電力ニュース
2017年4月号
電車線路設備耐震設計指針・同解説に未掲載条件の耐震性評価手法
~擁壁箇所に建植された電車線柱の応答加速度算定方法~
平成25年3月改訂の「電車線路設備耐震設計指針・同解説」(以下、耐震設計指針と記す)では、電車線柱が設備されている土木構造物の構造形式を、「高架橋・橋梁」と「盛土・切取」の2種類に分けて応答加速度の算定方法が示されていますが、「擁壁箇所」については明示されていません。そこで、擁壁箇所に建植された電車線柱の応答加速度の算定方法を提案したのでご紹介します。
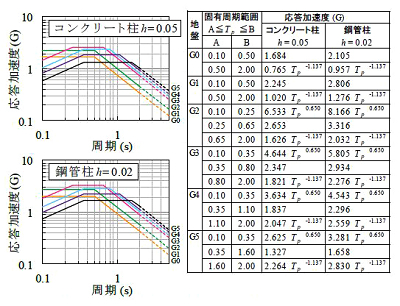
盛土・切取における電車線柱の応答加速度は、電柱基礎の塑性領域の特性を考慮した非線形応答解析により作成した加速度応答スペクトルにより算定しています。一方、擁壁箇所では、盛土・切取箇所より基礎部が強固であり、最も応答加速度が大きくなるのは電柱基礎が降伏しない場合と考えられます。このような擁壁箇所に建植されている電車線柱の応答加速度は、土木構造物の設計標準に示された弾性加速度応答スペクトルにより算定すれば最安全側であり、電柱基礎部が多少でも変形する場合は、それ以下の応答値になると考えられます。コンクリート電柱の減衰定数h は構造物モデルと同じ0.05 なので、上述の弾性加速度スペクトルを用います。また、鋼管柱(減衰定数h= 0.02)については、式(1) 1), 2)より、コンクリート柱の応答値SA(0.05)を補正して算定します。
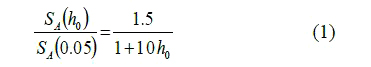
SA(h0):減衰定数がh0 での応答値式(1)より、減衰定数h0に鋼管柱の値(0.02)を代入すると右辺は1.25 となり、鋼管柱の応答値SA(0.02)は式(2)より算定できます。

図1 に、擁壁箇所に建植された電車線柱の加速度応答スペクトルを示します。なお、弾性加速度応答スペクトルは、スペクトルⅡの値がスペクトルⅠの値を包含しているので、電車線柱の応答値算定にはスペクトルⅡを用います。また、電車線柱の固有周期Tp は、高架橋・橋梁上の柱と同じ方法で算定します。
参考文献:
1) 田中,室野,鉄道総研報告,Vol.27,No.11,pp.17-22,2013
2) 平石,建築技術,No.614,pp.104-107,2001
(記事:電車線構造 常本 瑞樹)
電車線非接触測定装置の車載試験
鉄道総研では、電車線路設備の検査の効率化のため、測定手法の開発や診断の定量化の研究を行っています。特に、鉄道車両から測定を行うことで、長大な電車線路設備の効率よい検査が期待できます。
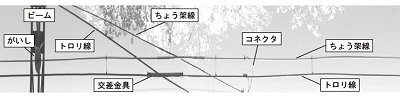
現在実用化を進めている電車線非接触測定装置について、図1に示すR291形試験電車の屋根上に図2のように測定器を搭載し、鉄道総研の所内試験線で測定試験を実施しました。この装置では、トロリ線だけでなく、ちょう架線なども含めた電車線の各線条の静的な位置を連続的に測定可能です。今回の試験では、車両の走行速度を最高で35km/h、ラインカメラのスキャンレートを5kHz、レーザー測域センサのスキャンレートを25Hzとしました。このとき、距離方向の測定ピッチは、ラインカメラで1.9mm/scan、レーザー測域センサで390mm/scanです。記録されるデータ容量は、画像を非圧縮で保存した場合、100km走行あたりおよそ1TB となります。また、高速なデータ転送が必要となるため、データ保存用のパソコンにソリッドステートドライブを使用しました。
図3に、所内試験線で測定した電車線の3次元位置を、図4に撮影した画像の例を示します。ここではジャイロで測定した車体のローリング角とレーザー測域センサの測定データから、車体動揺による影響を推定し、これを除去することで、動揺の影響の少ない測定が可能になりました。
今後は、高速走行時の安定した画像収録を目指し、ラインカメラやレンズの性能、照明の強度について検討を進めます。また、線条だけでなくハンガやコネクタなどに測定対象を拡大していくとともに、診断手法についても開発に取り組む予定です。
(記事:集電管理 松村 周)
等価12パルス整流器と電源電圧の高調波
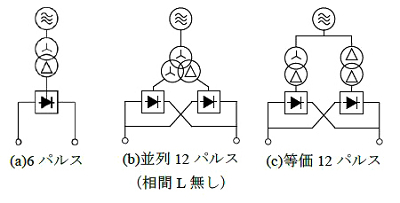
近年,直流き電変電所では、電力系統への高調波電流の流出を抑制し、高調波抑制対策ガイドラインに適合するために12パルス整流器の導入が進んでいます。新規に12パルス整流器を導入する方法の他に、6パルス整流器を2 台並列に運転し、等価12パルス整流器とする方法が有ります。このとき、2台の整流器の整流器用変圧器はΔ-ΔとY-Δのように互いに異なる巻線構造にします(図1)。
等価12パルス整流器では、2台の整流器の定格、変圧器のタップ、電圧変動率等を揃えて運転するのが原則ですが、2台の条件を揃えても整流器どうしの負荷電流が一致しない場合があります。この原因のひとつが、電源電圧に含まれる高調波です。
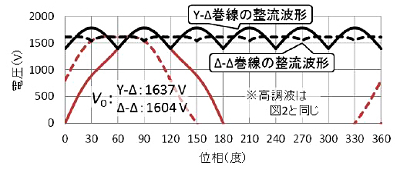
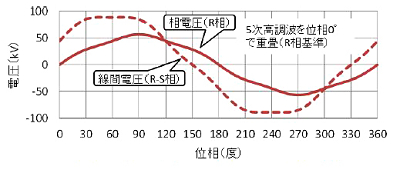
変圧器の巻線構造しだいで、整流器の交流側端子間には電源の相電圧または線間電圧どちらかに相似な波形の電圧が印加されます。ところが、高調波を含む電圧は、相電圧と線間電圧の波形が異なって見える場合があります(図2)。この影響で、整流された波形(図3)や、その平均値で表される無負荷直流電圧V0も2台の整流器で異なるケースが発生します。
整流器は、V0を開放電圧とし、ある出力抵抗をもつ電圧源としてモデル化できます。電源電圧に高調波が含まれる場合は、出力抵抗は同じでもV0 が異なる二つの電圧源を並列に負荷につなぐ事になるので、負荷電流が2台でアンバランスになってしまうのです(図4)。また、負荷が偏るということは、完全な12パルス整流動作となっていないことを意味し、本来は12パルス化で除去できるはずの高調波成分や電圧脈動が現れる場合もあります。なお、これらの現象は等価12パルス整流器に限らず、一体型の並列12パルス整流器でも同様に発生します。
高調波抑制対策ガイドラインによって規制はされているものの、電源電圧の高調波は依然として多く含まれる場合があり、抜本的な抑制対策は一般的に困難です。したがって、実運用上は12パルス整流器導入時には負荷の偏りをあらかじめ想定したり、直流フィルタの第1分路(6パルス整流に起因する電源周波数の6倍成分に同調)の省略は実際の波形を調査した上で検討したりといった配慮が必要です。
参考文献:
吉井剣:「電源高調波が等価 12 パルス整流器の負荷分担に与える影響についての一考察」,第23 回鉄道技術連合シンポジウム(J-RAIL2016),S3-3-4
(記事:き電 吉井 剣)
集電系ハイブリッドシミュレーション手法によるアクティブパンタグラフの性能評価
鉄道車両の更なる高速化に伴い、パンタグラフの更なる低騒音性が求められています。低騒音化には、気流に曝される部材の平滑化などが必要となりますが、これによりパンタグラフの追随機構を実現するために必要な空間に対する制約が大きくなる懸念があります。このようなケースにおける打開策として、鉄道総研ではパンタグラフをアクティブに制御することで架線との接触性能を向上させ、低騒音性と追随性を両立する手法を検討しています。
現在、アクティブパンタグラフの性能評価には、鉄道総研が所有するパンタグラフ加振装置を用いています。加振装置によりパンタグラフのすり板に決まった波形で強制変位を与え、制御により加振装置とパンタグラフ間の接触力変動が低減すれば制御性能が良好であると判断します。ただし、決まった波形でパンタグラフを加振するこのような試験方法では、制御により接触力変動が低減したことによって架線側の運動が変化する影響について考慮することができません。そこで、パンタグラフの定置試験でありながら架線との相互作用を考慮した試験がなハイブリッドシミュレーション手法(HS手法)を開発しました。
HS 手法は、「実機パンタグラフ」、「加振装置」と「架線運動シミュレーター」を連成させる手法で、加振装置と実機パンタグラフ間で実際に測定された接触力を架線運動シミュレーターに入力し、これに基づいて架線の運動を計算します。計算された架線の運動と同じ動きをするように加振装置を制御することで、実機パンタグラフに、架線運動シミュレーター内の架線モデル下を走行している状況と同じ運動をさせることができます。
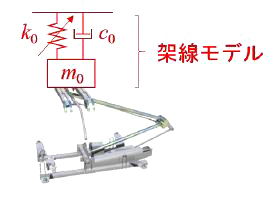
今回ご紹介するHS 手法による試験では、架線モデルとしてパンタグラフの走行位置に応じて架線の剛性が変化する係数励振モデル(図1)を適用しています。図1のモデルは、径間周期(電柱間隔)に起因する運動を主に表現することができるモデルです。本アクティブパンタグラフは、径間周期の運動に起因する接触力変動を低減することが目的であるため、本HS手法により着目したい現象に特化した性能評価試験を行うことができます。
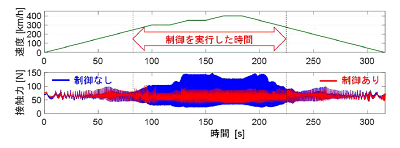
前述のアクティブパンタグラフが図1のモデルで表現された架線の下を図2の上図に示すランカーブで走行した際の接触力の時系列波形を、図2の下図に示します。アクティブパンタグラフの制御測としては、電力ニュース第97号に紹介されたフィードフォワード制御を用いています。図2の下図より、制御によって接触力変動が大幅に低減されており、アクティブパンタグラフによる径間周期の運動に起因する接触力変動の低減効果を確認しました。
(記事:集電力学 山下 義隆)