シートパイル基礎の設計・施工マニュアルの改訂
1.はじめに
シートパイル基礎工法は、2006年に鉄道総研と大林組の2社が共同研究により開発した工法で、その後、鉄道総研と新日鐵住金により軟弱地盤でも適用が可能な「先端支持型シートパイル基礎工法」を開発しています。既存のマニュアルとして、①「鉄道構造物に適用するシートパイル基礎の設計・施工マニュアル(第2版)」(2006年発行)、②「シートパイルを用いた既設鉄道構造物基礎の耐震補強設計マニュアル(案)(第2版)」(2011年発行)、③「先端加工鋼矢板を用いた先端支持型シートパイル基礎設計・施工マニュアル(案)」(2011年発行)を作成しておりますが、今回このうち、①・③の設計施工マニュアルにつき1冊にまとめ、「鉄道構造物に適用するシートパイル基礎の設計・施工マニュアル(案)(第3版)」(以下、「新マニュアル」)とし、改訂しました。ここでは、改訂したマニュルについて紹介します。
2.改定の概要
「鉄道構造物等設計標準・同解説(基礎構造物)」が、2012年に性能規定型の設計法に改訂され、新たに「17章 その他の基礎」において新しい基礎形式として「シートパイル基礎工法」が導入されました。新マニュアルは、この鉄道標準の改訂に対応するとともに、より実務者向けに具体的な設計・施工の取扱いをとりまとめたものです。
具体的な改定内容は以下の通りです。
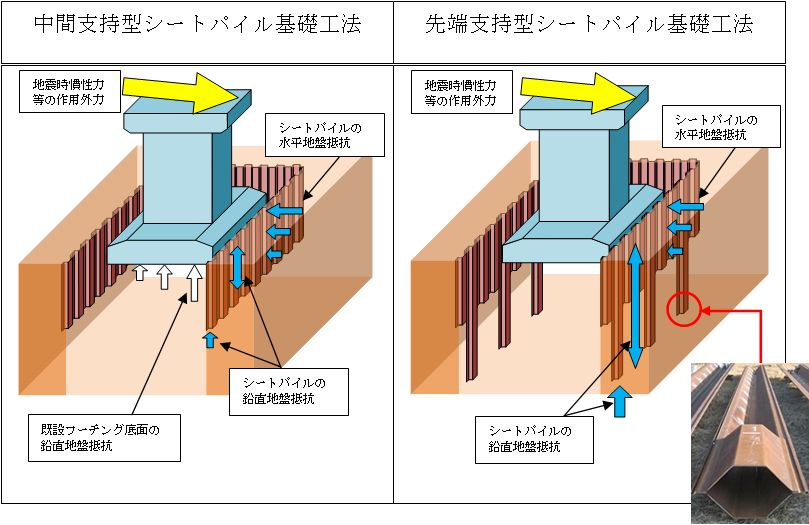
図1 シートパイル基礎工法の種類
(1)地盤ばねの改訂
前背面シートパイルの水平地盤抵抗は、寸法効果として鋼矢板幅の-3/4乗が考慮された算定式が示されていたが、ケーソン基礎の算定式に準拠するように改訂しました。これにより比較的小規模の構造物にのみ適用可能だったものを従来よりも大きな基礎へも適用範囲を拡大しました。
また、シートパイルの鉛直方向のせん断地盤抵抗については,改訂前ではH鋼杭の算定式に準じるとしていましたが,基礎標準の改訂に合わせて打ち込み杭工法の地盤抵抗算定式に改訂した。
さらに、側面シートパイルの水平せん断地盤抵抗は,改訂前では鉛直方向と同一としていましたが,砂質土であればシートパイルの凹凸による断面形状を考慮することにより,鉛直方向(鋼材表面と地盤とのせん断抵抗)よりも大きくなるため、これを取り入れ,砂質土の場合には割増係数βs=1.7を乗じることとしました。
(2)先端支持型シートパイル基礎の追加
中間支持型シートパイル基礎のように、中間層に中間支持可能な層がない場合に深部の支持層に支持させた先端支持型シートパイル基礎をマニュアルに追加しました。この工法では、鋼矢板の先端を加工し、鋼管杭のように先端閉塞させることで、通常の鋼矢板に比べ、より大きな先端支持力を発揮することが可能です。(図1)

写真1 マニュアル
写真2 講習会開催状況
3.おわりに
シートパイル基礎は,仮土留めに用いるシートパイル(鋼矢板)とフーチングを組み合わせた複合基礎であり,低コストで施工性に優れた工法です.設計には注意すべき事項がありますが,施工実績もあり,耐震性の向上および経済化にも期待できます。5月にはシートパイル基礎の講習会も開催しましたが、今後も更なる普及に努めていきたいと考えています.シートパイル基礎をご検討の際には,マニュアルに記載の連絡先または,基礎・土構造研究室まで必ずご連絡いただけますようお願い致します。
(記事:松浦光佑)
列車通過後の残存波形に基づく構造パラメータの同定手法
1.はじめに
高度経済成長期に建設された多数の鉄道橋に対する効率的な維持管理の実現には,簡易な調査に基づく状態評価手法が必要となります.鉄道橋の振動特性1)(固有振動数やモード減衰比)は,構造形式に依らず取得可能な構造パラメータであり,注意すべき鉄道橋の1次的なスクリーニングへの活用が考えられます.これまでは衝撃加振試験に基づき振動特性を評価(同定)することが一般的でしたが,最近では非接触測定技術2)も一般化しつつあり,走行列車を加振源として利用して振動特性を評価できれば,測定・状態評価の効率が飛躍的に向上します.本稿では,このような走行列車を用いた試験からでも,振動特性を高精度に同定する方法を検討したのでご紹介します.
2.検討方法
図1に分析対象波形を示します.列車通過時のたわみ波形の中でも鉄道橋自体の振動成分が支配的となる列車通過後の残存波形を対象とします.図2には提案手法であるARS法と比較対象である3つの同定手法を示します.高速フーリエ変換に基づくスペクトルを用いるのが最も一般的な方法(FFTS法)ですが,列車通過後の波形に混入したノイズ成分を低減するために,自己回帰(AR)モデルに基づくスペクトル(ARS)を用いる方法がARS法です.本稿では,ARS法と既存の同定方法(FFTS法、AR法、1DOF法)をそれぞれ新幹線用鉄道橋の測定結果に適用することで比較検証を行いました.なお,AR法と1DOF法は,それぞれ固有値分解とカーブフィットにより波形から固有振動数とモード減衰比を同定します.
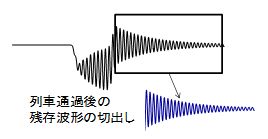
図1 分析対象波形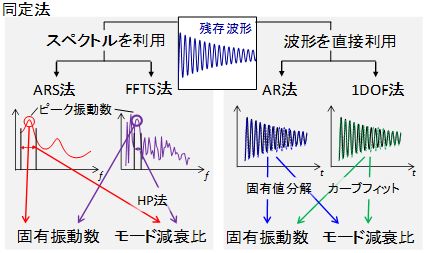
図2 同定手法
3.検討結果
図3にARS法とFFT法でそれぞれ算出したスペクトルを示します.FFT法に見られるノイズ成分に起因した細かいピークがARS法では大幅に低減されています.また,図4には全348ケースの中で各同定手法により同定結果が得られた割合を示しています.ARS法は,他手法と比較して1割程度多い約8割のケースで同定結果が得られていることがわかります.
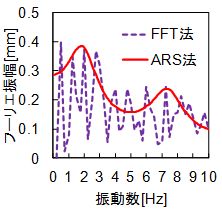
図3 ARS法によるノイズ低減効果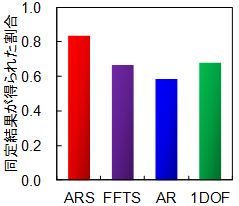
図4 同定結果が得られた割合の比較
図5から図7には列車速度と進行方向が同定結果に及ぼす影響の例として,PC単純ホロー桁,PC単純下路桁,PC連続箱桁の同定結果をそれぞれ示しています.また,同図右には,平均と標準偏差を手法ごとに示しています.図5のPC連続ホロー桁におけるAR法や,図6のPC単純下路桁における1DOF法の適用結果は,列車速度への依存性も見られずばらつきも小さくなっていますが,他の鉄道橋での同定結果では,大きくばらついてしまっています.一方,ARS法ではいずれの鉄道橋へ適用した場合でもばらつきが小さいうえ,列車速度や進行方向への依存性も見られず,精度の高い手法であることがわかります.
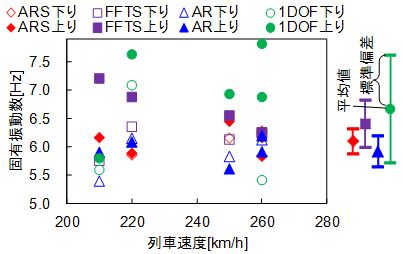
図5 走行列車によるばらつきの比較
(PC単純ホロー桁:径間長20m)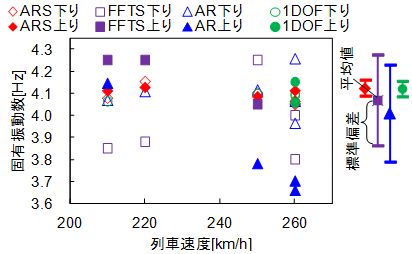
図6 走行列車によるばらつきの比較
(PC単純下路桁:径間長40m)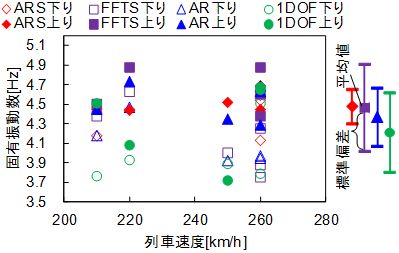
図7 走行列車によるばらつきの比較
(PC連続箱桁:径間長34.3m)
図8は,ARS法で同定した全348ケースの固有振動数 f と径間長 L の関係を示します.固有振動数 f は径間長L-0.8で整理されることが多く,本検討の結果も径間長Lに対して f =70L-0.8の曲線付近に集中すること,固有振動数の下限は概ね f =55L-0.8で表わされることがわかります.また,これらの結果は過去の検討事例3)とも整合的となっています.
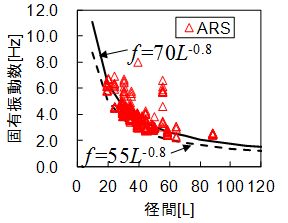
図8 固有振動数と径間長の関係
図9は,各手法で同定した全348ケースのモード減衰比と径間長 L の関係を示します.同図にはEurocodeで示されているコンクリート鉄道橋のモード減衰比を合わせて示しています.同図からは,どの手法を用いてもある程度のばらきが生じるものの,AR法および1DOF法の結果と比較して,ARS法とFFTS法では安定した同定結果が得られていることがわかります.モード減衰比のばらつきの要因については,数値解析などを利用して今後詳細に検討していく予定です.
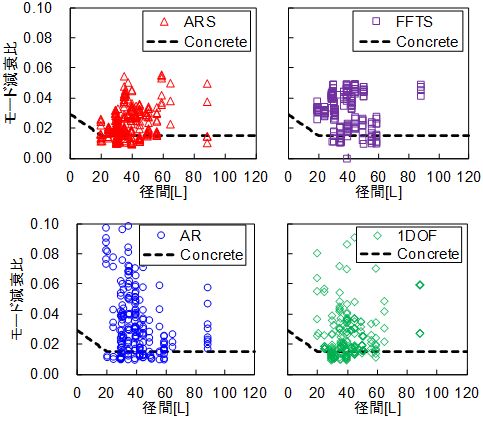
図9 モード減衰比の同定結果と径間長の関係
4.おわりに
今回紹介したARS法を活用することで,走行列車の特性が混入する列車通過後の残存波形からでも,固有振動数を安定して高精度に同定することができます.また,本手法とUドップラー等の非接触測定システムを組み合わせることで,効率的な既設鉄道橋の構造パラメータの収集ができるようになると考えています.今後は,測定事例を継続的に蓄積するとともに,鉄道橋の種別や状態との関係についてより詳細に分析していく予定です.
参考文献
1) 松岡弘大,貝戸清之,渡辺勉,曽我部正道:走行列車荷重を利用したRC鉄道高架橋の部材振動の同定と動的挙動の把握,土木学会論文集A1,Vol. 67,No. 3,2011
2) 上半文昭:構造物診断用非接触振動測定システム「Uドップラー」の開発,鉄道総研報告,Vol. 21,No. 12,2007
3) 鉄道総合技術研究所編:鉄道構造物維持管理標準・同解説(構造物編)コンクリート構造物,丸善,2007
(記事:松岡弘大)
新幹線用レール鋼製ノーズ可動クロッシングの開発
1.はじめに
現在,新幹線用分岐器のノーズ可動クロッシングは,粘り強く割れにくく耐摩耗性に優れているといった特徴がある高マンガン鋼で製造されています.ただし,高マンガン鋼は,鋳鉄鋼であることから内部に鋳巣と呼ばれる微細な空隙が介在することがあります.この鋳巣を完全に除去することは難しく,また超音波探傷検査が困難なために,内部の傷の進展を把握できません.
そこで,超音波探傷検査が可能で,前後のレールとの溶接が容易であるレール鋼を用いたノーズ可動クロッシングを開発しました.
2.構 造
高マンガン鋼製ノーズ可動クロッシングは,ウィングレール,可動レール,クロッシング構の3要素で構成されています(図1).ウィングレールの基準線側の前端は斜め継目の構造となっています.可動レールは,基準線側のみ弾性部を設け,また,基準線側の後端は伸縮構造となっています.一方,開発したレール鋼製ノーズ可動クロッシングは,ウィングレール,可動レール,大床板の3要素で構成されています(図2).ウィングレールは,80Sレールを使用し,基準線側の前端は高マンガン鋼製と同様に斜め継目の構造になっていますが,溶接継目に変更可能です.可動レールは,80Sレールをアーク溶接で接合した二叉レールと,特殊断面形状の100Kクレーンレールをガス圧接にて接合したレールから削り出して製作しています.また,基準線側の後端部は,新幹線用伸縮継目と同じ構造となっており,分岐線側の後端部は,転換時に発生するふく進を吸収するために,簡易型伸縮構造となっています.さらに,転換動作を滑らかにするため,基準線側と分岐線側の両方に弾性部を設けています.大床板は,1枚の鋼板から削り出し,可動レールを1枚の床板で支えることによって,発生する応力を軽減させるような構造となっています.この大床板上に,ウィングレールや可動レール等のレール類と部品類等を配置し,簡単に組み立てることができる構造になっています.
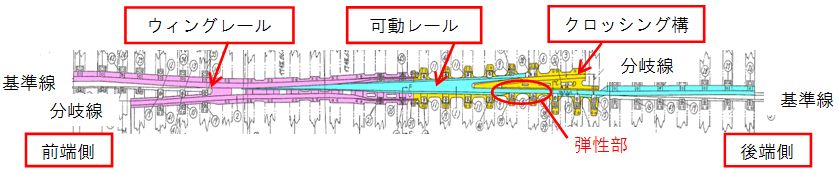
図1 高マンガン鋼ノーズ可動クロッシングの構成
図2 レール鋼製ノーズ可動クロッシングの構成
3.性能確認
まず,転換時の可動レールの挙動,発生応力および変位を把握するため,可動レール単体での静的解析および転換試験を実施しました.転換条件は,基準線側の後端部を完全固定した状態で,分岐線側の後端部を固定した場合(条件①)と固定しなかった場合(条件②)としました.条件①では,解析は分岐側の弾性部に,許容応力の目安値である137N/mm2を超える著大な応力が発生し,試験では,基準線側と分岐線側にほぼ均等に応力が発生しました.また分岐線側の後端部を固定していたにも係わらず,前端側へ2.0mmふく進し,さらに元の位置まで再び転換しても0mmに戻りませんでした.一方,条件②では,解析と試験の結果が同等の値となり,基準線側と分岐線側の弾性部にほぼ均等の応力が発生しました.さらに元の位置まで再び転換したところ,2.5mmあったふく進は0mm戻ることを確認しました.これらのことから,可動レールを完全に固定することは困難であると判断し,ふく進を吸収する簡易型伸縮構造(図3)を設けることにしました.この簡易型伸縮構造は,既存の伸縮継目と同様な構造ですが,伸縮量は想定されるふく進を考慮して小さくし,後続のレールがふく進しても,軌間が変化しない構造になっています.その後,新幹線用レール鋼製ノーズ可動クロッシング全体を試作(図4)して,転換試験を実施し,問題なく転換されていることを実証しました.
- 表1 静的解析と転換試験結果
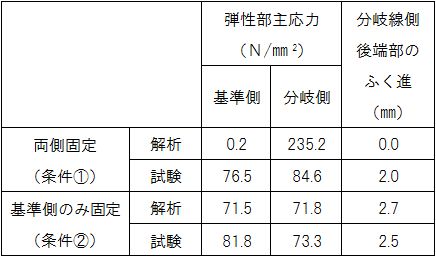

図3 簡易型伸縮構造
図4 試作したレール鋼製ノーズ可動クロッシング
4.試験敷設
試作した新幹線用レール鋼製ノーズ可動クロッシングを鉄道総研の日野土木試験所内に敷設し,載荷試験およびモータカーによる走行試験を実施しました.載荷試験では,移動式軌道動的載荷試験装置を用いて,鉛直方向に最大100kNの荷重を与え,発生応力や変位を測定した結果,問題となるような大きな応力や変位が発生しないことを確認しました.また,走行試験では,基準線側開通状態で,モータカーを30km/h程度で走行させ,問題なく通過できることを確認しました.

図5 載荷試験風景
5.おわりに
転換試験,載荷試験および走行試験を実施し,今回開発した新幹線用レール鋼製ノーズ可動クロッシングの構造に問題のないことが確認できました.今後,実用化に向けての取組みを継続して行きます.
(記事:原田 茂幸)
