電力ニュース

• 車上・地上間同時電流測定による地絡検知アプリケーションの基礎検証
• 電車線のレール方向変位計算モデルの妥当性確認のための模型試験
• アルミニウム合金製電車線柱の耐震設計
• 光切断式トロリ線摩耗計測の高速度域における精度検証
• 【ワンポイント講座】交流の電圧・電流の実効値

車上・地上間同時電流測定による地絡検知アプリケーションの基礎検証

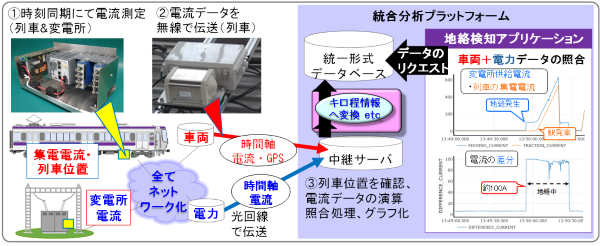
　電車線路への設備追加を行わずに直流電気鉄道における高抵抗地絡故障を検知する実用的な手法はまだ確立されていません ¹⁾。このような手法の一例として変電所のき電電流（地上）と列車の集電電流（車上）とをキルヒホッフの電流則に基づいて照合し、その差分が大きい場合は地絡故障発生と見做す検知手法 ²⁾が以前から提案されていますが、ICTを活用してこの手法を具現化すべく、地上・車上各々の電流値データにタイムスタンプを付して伝送する直流電流計測システムを製作した ³⁾ほか、車上の電流値データや列車位置などの情報を無線システムで地上のデータサーバに逐次送信することが可能となりました。

　今回、上記成果を活用した地絡検知アプリケーション（以下、地絡検知アプリ）の開発と検証を行い、地絡判定が可能であることを実証したので、その特徴を紹介します。開発にあたり、車上と地上という複数系統のデータを一元管理するべく、図1に示す統合分析プラットフォーム（以下、分析PF）を活用しました。また、地絡検知アプリは分析PF上に構築し、分析PF自体が有するデータ演算機能やグラフ作成機能などと連系させました。地絡検知アプリが具備する主な機能は次の通りです。
・指定された電力供給区間における車上・地上各々の電流値データデータを逐次集約する機能
・キルヒホッフの電流則に基づく電流照合のため分析PFの四則演算モジュールなどを呼び出す機能
・指定した期間における電流差分の積算結果（差分積算値）をもって地絡判定演算する機能

　鉄道総研の所内試験線において、1列車・1変電所という基礎的な条件にて、試験列車走行中に100アンペア程度の地絡故障が生じた場合を模擬した電流データ等を地絡検知アプリで分析しました。その結果、図2に示すように地絡中に生じる100アンペア程度の電流の差分を地絡検知アプリにて適切に把握することが出来ました。今後は、より営業線に近い模擬として、電力供給区間や列車が複数存在する条件で検証試験を行う予定です。

[参考文献]

• 1) 森本大観：森本大観：直流き電回路の高抵抗地絡保護への取り組みと課題、JREA、Vol.60、No.10、pp.15-19、2017.10
• 2) 電気学会技術報告（II部）第542号、p.65、1995.5
• 3) 赤木雅陽：高精度時間プロトコルに対応した直流電流計測システムの基礎検討、鉄道総研電力ニュース、Vol.118、2022.4

電車線のレール方向変位計算モデルの妥当性確認のための模型試験

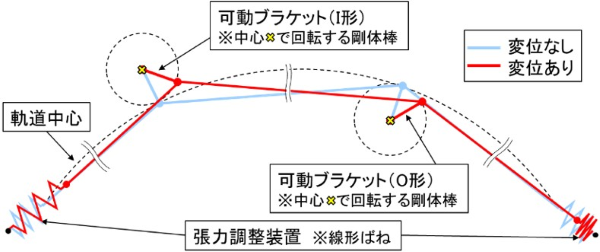
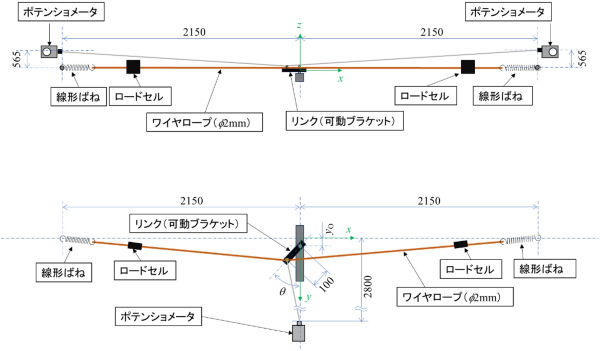
　電車線のレール方向変位は様々な要因で生じます。既報 ¹⁾では、可動ブラケットが電車線のレール方向変位の偏りに与える影響を数値計算により調査した結果についてご紹介しました。本稿では、計算に用いたモデルおよびそのモデルの妥当性を検証した模型試験について紹介します。当該の計算では、ヨークで一括に引き留められているちょう架線とトロリ線を１本の線条でモデル化しました。両端の張力調整装置および引留区間内の可動ブラケットは、図1に示すように、線形のばね要素および回転を許容する剛体棒でモデル化しました。引留区間内の可動ブラケットのI形およびO形は曲線軌道の外側および内側に回転中心を置くことでその違いを表現しました。モデルの妥当性を確認するための模型試験の概略図を図2に示します。この模型試験では、引留区間内に単一の可動ブラケットを配置した状況を再現しています。ブラケットを模擬したリンクの回転中心のy座標（図2中のyo）の位置を変えること、すなわちリンクの回転中心と引留点（線形ばねの固定端）との位置関係を変えることは、I形・O形および曲線半径を変えることに相当します。張力調整装置を模擬した線形ばねのばね定数、曲線半径およびI形・O形の条件を変え、リンクに初期角度を与えてからリンクの拘束を解き、リンクの角度がとる最終値までをポテンショメータで測定した。リンクの最終角度について、実験結果と計算結果を比較した表を表1に示します。実験結果と計算結果は数度の誤差に収まっており、計算モデルの妥当性が示せたと考えています。この方法で表現した電車線モデルにより、電車線流れの現象解明などに役立てたいと考えています。

[参考文献]

• 1) 山下義隆、可動ブラケットが電車線のレール方向変位に与える影響、鉄道総研電力ニュースNo.121、2023
• 2) 山下義隆ら、電車線の長手方向変位に対する平衡点計算法、日本機械学会論文集、Vol.90、No.932、2024

アルミニウム合金製電車線柱の耐震設計

　アルミニウム合金（以下、アルミ合金）は軽量かつ耐腐食性が高いため、電車線柱（以下、電柱）に適用することで施工性や保守性の向上が期待できます。しかし、アルミ合金製電柱を耐震設計する際に必要な(1)曲げモーメントの限界値、(2)固有周期補正乗率、(3)加速度応答スペクトルが不明であるため、導入が検討されている6000系アルミ合金製継目無管（以下、アルミ柱）を対象に、これらについて検討を行いました ¹⁾。

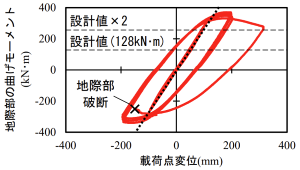
　(1)　曲げモーメントの限界値 アルミ柱の交番載荷試験結果（図1）より、地際部の曲げモーメントの最大値は、アルミ柱の設計曲げモーメント（図中の設計値）の2倍に対して十分に余裕があることから、アルミ柱の曲げモーメントの限界値は、鋼管柱と同様に、設計値の2倍と設定して問題ないことを確認しました。

　(2)　固有周期補正乗率 電柱の固有周期T _pは、単体の電柱の固有周期に固有周期補正乗率を乗じて算出します。固有周期補正乗率には、①電柱に取り付けられた電線や架線金具（以下、添架物）の質量による影響を補正するα_Wと②曲げ剛性の低下による影響を補正するα_Rがあります。 ①については、在来線を想定した装柱条件のアルミ柱の実験結果より、添架物の質量が与える影響がコンクリート柱や鋼管柱に比べて大きくなることを確認しました ¹⁾。 ②については、アルミ柱の交番載荷試験結果（図1）より、地際部の曲げモーメントに対する載荷点変位の変化（図1中の黒破線）が曲げモーメントの限界値（設計値の2倍）まで一定であることから、曲げ剛性の低下による影響を考慮する必要がないことを確認しました。

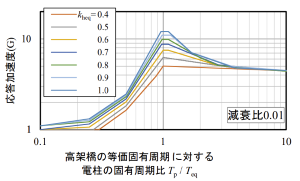
　(3)　加速度応答スペクトル アルミ柱と類似した構造物のアルミ合金製照明ポールで用いられている減衰比0.01を採用して、アルミ柱の加速度応答スペクトルを作成しました（図2）。

　これらの結果を用いることで、電車線路設備耐震設計指針 ²⁾に基づいたアルミ柱の耐震設計が可能になります。ただし、今回対象とした在来線の装柱条件以外の場合や6000系以外のアルミ合金を素材とする場合は、上記(1)と(2)を確認する必要があります。

[参考文献]

• 1) 近藤優一ら：アルミニウム合金製電車線柱の耐震設計、JREA、Vol.66、No.12、2023
• 2) 鉄道総合技術研究所：電車線路設備耐震設計指針・同解説、2013

光切断式トロリ線摩耗計測の高速度域における精度検証

　光切断法は、帯状のレーザー光を計測対象に照射し、反射光をカメラで撮影して対象物の断面形状を計測する手法です。この手法を用いることで、トロリ線の摩耗断面積が計測可能であり、必要により残存直径に換算できます。

　電力ニュースNo.106（2018年4月号）にてトロリ線摩耗測定手法の基礎検討について紹介しましたが、この手法を用いた計測装置を新幹線車両に適用する場合、高速走行によるトロリ線ジグザグ偏位や高さの変化、およびトロリ線局部摩耗に伴うトロリ線大弧面の形状変化などによって、光切断像を取得する際に画像のブレ（被写体ブレ）が生じ、トロリ線の摩耗計測精度に影響を及ぼす可能性があります（図1）。

　そこで、トロリ線ジグザグ偏位、高さ、局部摩耗による相対的なトロリ線の移動量・形状変化量の検討、高速度域を模擬した環境でのトロリ線摩耗計測試験により、高速度域での被写体の変動がトロリ線の摩耗計測精度に及ぼす影響を調査しました。

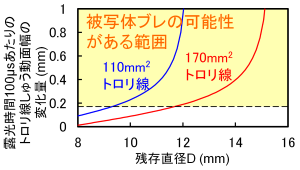
　検討の結果、ジグザグ偏位や高さ変動等のトロリ線移動については、360km/h走行時においてもシャッター速度に対して被写体移動量が小さいため、被写体ブレが発生しないことがわかりました。一方、局部摩耗等のトロリ線の形状変化については、残存直径が比較的大きいときに局部摩耗の勾配に起因した被写体ブレが発生する可能性があることがわかりました（図2）。

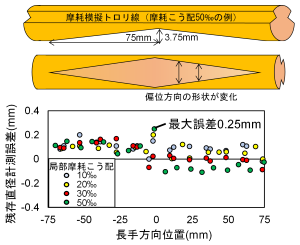
　上記の検討結果をふまえ，トロリ線局部摩耗に起因した形状変化による被写体ブレが摩耗計測精度に及ぼす影響を調査しました。試験の内容は、鉄道総研所内の回転試験装置に、局部摩耗を模擬したトロリ線と、形状測定のためのカメラとレーザー光源を設置し、トロリ線を360km/hで回転させて高速度環境下での摩耗計測精度を検証するというものです（図3）。

　現地における局部摩耗の勾配は過去の文献調査から最大14‰と想定されたため、10～50‰の勾配をもつ局部摩耗を模擬して摩耗計測試験を行いました。その結果、いずれの条件でも残存直径の計測誤差が±0.3mm以内であることがわかりました（図4）。

　以上の結果から、光切断式トロリ線摩耗計測では360km/hの高速度域においても、十分な摩耗計測精度を確保できることが確かめられました。現在、上記内容を含めた知見に基づき、同計測装置の実用化に向けた技術支援を実施しています。

【ワンポイント講座】交流の電圧・電流の実効値

　交流の電圧や電流を測定する際、実効値という指標をよく使います（以下、電圧と電流とで共通ですので、電圧のみを取り上げます）。この実効値の定義は、「ある電気抵抗に交流電圧を加えた場合にその交流波形１周期において電気抵抗によって消費される平均電力と、同じ抵抗に直流電圧を加えた場合の電力が、互いに等しくなるような、電圧の値」と定義されています。ここで、この実効値の定義における「交流電圧」自体には、特定の波形のみを前提とする規定は含まれていないことに着目しましょう。

　一方、ある交流電圧の記録波形からその実効値を求めるにあたり、漫然と、かつ頻繁に行われてしまっている簡易換算方法として、「波形のピーク値（片振幅）を√2で除す」「波形のピークtoピーク値（両振幅）を2√2で除す」という行為があります。これには注意が必要です。実は、この簡易換算方法を使用してよいのは、元の波形が単一周波数の正弦波（高調波や分数調波などが含まれない）である場合のみに限られており、この条件が満たされない状況における簡易換算方法の使用は望ましくありません。

　交流き電回路の電圧・電流には、高調波が含まれていることが大半です。交流き電回路に高調波拡大現象があることは広く知られていますが、そのことなども考慮すると、高調波が含まれる機会が多いき電回路の電圧・電流記録波形に対して片振幅を√2で除す・両振幅を2√2で除す簡易換算方法を用いると、往々にして誤った結果を得てしまうことになります。実効値の正確な定義に基づき、波形1周期についてその中の全サンプル点の値を2乗（square）したものを算術平均（mean）し、その平方根（root）を実効値とする必要があります。（電力は電流の二乗と抵抗の積であるためこうなります。実効値の略語RMSは、二乗平均平方根Root-Mean-Squareから来ています）。

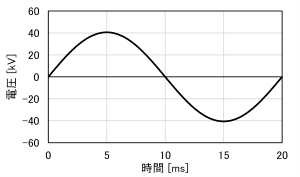
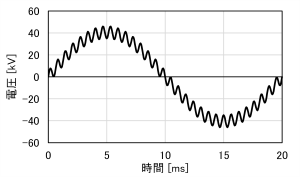
　一例として、基本波周波数50Hzにおいて、実効値28.7kVの正弦波交流電圧波形（高調波を含まない）を図1に、また、それに実効値4kV・位相零の31次高調波を重畳した波形を図2に、それぞれ示します。図2の波形は、正確な定義による実効値（小数第二位までで四捨五入丸め）は28.98kVですが、片振幅を√2で除した簡易換算値（同）は32.52kVとなります。

　電力供給能力視点での過電圧・不足電圧を論じるときに、正弦波ではない波形（矩形波・台形波、三角波、高調波が含まれる波形など）に対しては、簡易換算は避け、正確な定義で実効値を算出することが望ましいです。一方、避雷器やがいしにおける絶縁協調を論じるときには、電力供給能力視点と異なりピーク電圧のほうが重要であり、議論の対象に応じて実効値・ピーク値を使い分けることが必要です。

　なお、実効値のほかに、整流平均という別の指標もありますが、これは別の機会に紹介いたします。