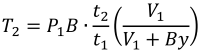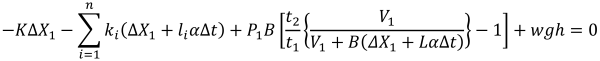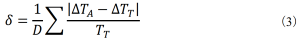電力ニュース

• ステレオカメラによる3次元電車線振動測定
• 両端に異種のバランサを用いた場合のバランサ伸縮量計算
• トロリ線とすり板の摩擦熱による接点の温度上昇解析モデル（１）
• 直流き電回路を用いた再エネ電力送電の可能性
• 【ワンポイント講座】大型低騒音風洞を活用したパンタグラフ揚力の測定

ステレオカメラによる3次元電車線振動測定

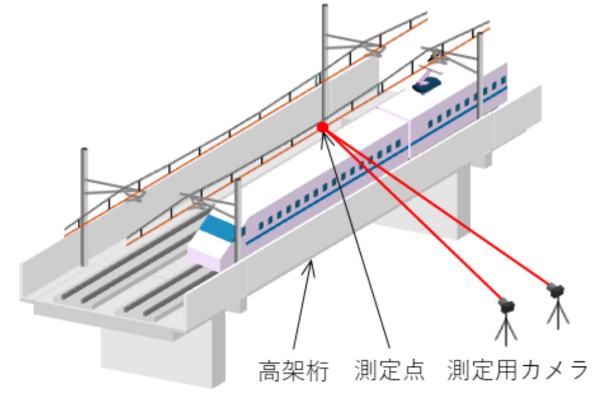
　列車通過時にはパンタグラフによる押し上げを主要因として電車線に振動が生じます。新線区開業時の安全確認等の場面でこの振動の測定が求められることがあり、測定対象に変位センサ等を直接取り付けて測定する方法が一般的です。しかし、本方法では測定機器の仮設・撤去のために停電作業や線路内立ち入りが必要となり、多大な労力が掛かります。そこで、鉄道総研では図1のように線路外から電車線の振動を2台のカメラ（ステレオカメラ）で撮影し、取得した動画データを解析することによって電車線の3次元振動を測定する手法を開発しています。測定原理は次の通りです。

(1)各カメラで取得した動画にデジタル相互相関法（図2）を適用し、各フレーム（時刻）での測定対象点の画像上の位置を導出
(2)2つの動画から得られた位置とカメラの特性から、三角測量の要領で測定点の3次元座標を復元

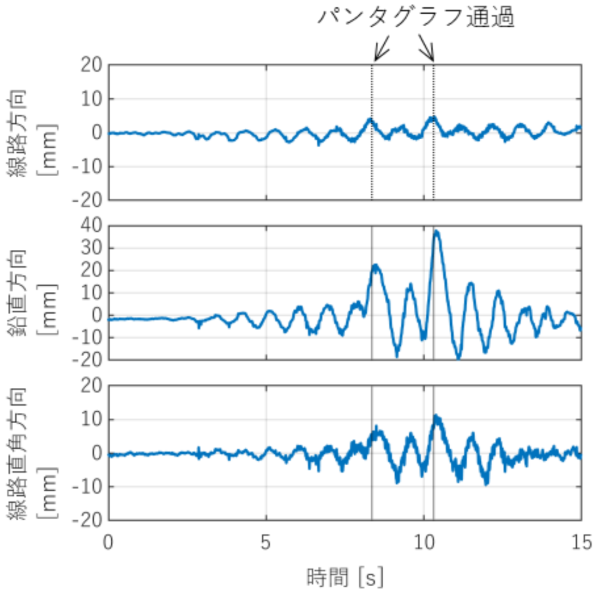
　図3に高架橋振動区間での列車通過時のトロリ線の振動測定結果の例を示します。高架橋および電柱の振動に起因する電車線の線路方向の振動や、パンタグラフによるトロリ線の押し上げ（鉛直方向変位）を捉えることができています。現在、本測定手法の測定精度の検証を進めています。

両端に異種のバランサを用いた場合のバランサ伸縮量計算

　電車線の設計では、バランサの可動限界に到達することのないよう、電車線の温度伸縮を考慮してバランサを選定します。バランサの種類には滑車式（以後、WTB）やばね式（以後、STB）に加え、温度変化に伴うガスの膨張収縮を利用したガス式（以後、GSTB）があります。GSTBは小型軽量で設置工事の労力が少ないため、例えば両引きSTBの電車線において片側のSTBを交換する必要が生じたときにGSTBに変更することで施工上の利点があると考えられます。しかし、異種のバランサの組み合わせの可否はこれまでにあまり検討されていませんでした。そこで、その可否を判断可能とする計算方法を考案しました。

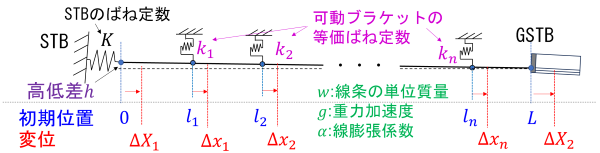
　バランサの伸縮量計算モデルを図1に示します。本モデルは、電車線を等価な1本の線条とみなし、引留区間内の可動ブラケットを等価ばねに置き換えたものです ¹⁾。なお、可動ブラケットの等価ばね定数はO型ブラケットの場合は負、I型ブラケットの場合は正となります。ここでは、左端をばね定数KのSTB、右端をGSTBとしています。また、本計算モデルでは伸び剛性が十分に大きいと仮定して弾性伸びの影響を無視し、GSTBは温度変化後の張力T₂が、

であらわされるとします ²⁾。ここで、Pはガス圧力、VはGSTB内部のガス体積、tはガス温度、Bはロッドの受圧部面積、yは電車線の伸縮によるロッドの変位量とし、添え字の1は温度変化前の値、添え字の2は温度変化後の値であることを示します。電車線の線路勾配を考慮するため、電車線左端と右端の高低差をhとします。電車線左端の変位をΔX₁とおき、温度変化をΔtとすれば、任意の初期位置xにおける変位Δxは Δx = ΔX ₁+ x α Δtと表され、左からi番目の可動ブラケットの温度変化後の変位はΔl_i = ΔX₁ +l_i α Δtとなります。以上の設定に基づき、線条全体の力のつり合いを考慮すると下記の式となります。この式は未知数 ΔX₁に対する非線形方程式であるため、ニュートン法等により求解します。Δx =ΔX₁+ x α Δtに求めたΔX₁を代入すれば任意の位置における変位が求まります。

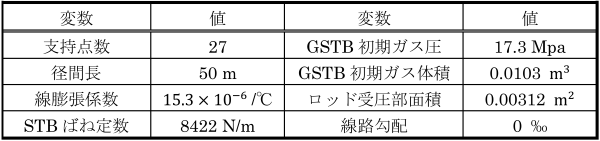
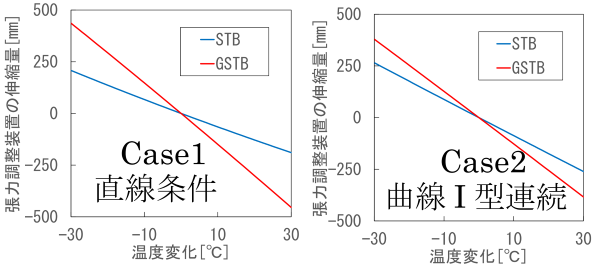
　表1に計算に用いた設備条件を示します。この設備条件に対し、全区間直線の条件（Case1）と、電車線の中央を境にSTB側が直線、GSTB側が半径1500mの曲線かつI型ブラケットが連続する条件（Case2）におけるSTBおよびGSTBの伸縮量を計算した結果を図2に示します。Case1では両端のバランサの張力変動特性の差によってGSTB側の伸縮量が大きくなってしまいますが、Case2ではその影響が小さくなり、このような条件では異なる種類のバランサを使用できる可能性があります。このように、本稿で示した計算方法は、様々な条件に対応したバランサの伸縮量を計算することが可能であり、施工区間の条件に応じた適切なバランサの選定に活用できると考えられます。

[参考文献]

• 1)社団法人日本鉄道電気技術協会 : 電車線〔Ⅱ〕，pp.99～106，2008
• 2)武藤洋，他：ガスばね式張力調整装置における集電性能の評価，鉄道総研報告，Vol.32，No.4，2018

トロリ線とすり板の摩擦熱による接点の温度上昇解析モデル（１）

　トロリ線やすり板などの集電材料は、主に摩耗によって寿命を迎えます。集電材料の摩耗は、電気的要因以外に機械的摩耗があり、機械的摩耗に影響を及ぼす大きな要因は摩擦熱による温度上昇です。そこで、摩擦熱によって接点温度がどれだけ上昇するのかについて解析モデルを構築しました。

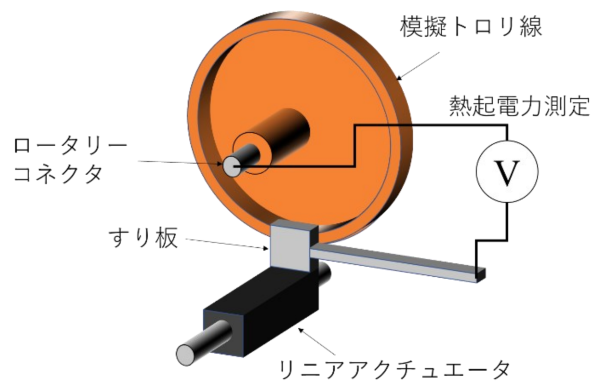
　実験に使用した回転摩耗試験機 ¹⁾を図1に示します。硬銅トロリ線と同等の特性をもつ銅円盤を模擬トロリ線とし、鉄系焼結合金すり板試験片を押し当てて、しゅう動させました。トロリ線とすり板の接触境界にある真実接触点 ²⁾の温度は、図1中の熱起電力から測定しました。この熱起電力から推定した温度の妥当性は、材料の硬さ測定などで検証しています ¹⁾。

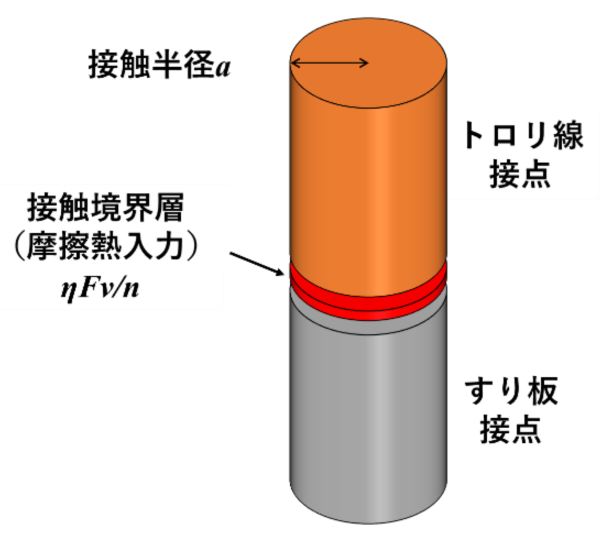
　トロリ線とすり板の真実接触点（接点）の温度上昇解析モデルを図2に示します。このモデルは、それぞれの接点を円柱とし、その中間に接触境界層として、摩擦熱を入力する層を設定しています。入力する摩擦熱W_f[W]は、実験で得られた摩擦力F[N]、速度v[m/s]から、次式で計算しています。

ここで、ηは係数、nは接点の個数です。解析モデルの接触境界層に摩擦熱を入力し、円柱の半径a[m]から　式(2)で計算した接点同士が接触する時間t[s]で上昇する接点温度を非定常熱伝導解析で計算しました。なお解析モデル上、接点は相対滑り等の動きはしません。

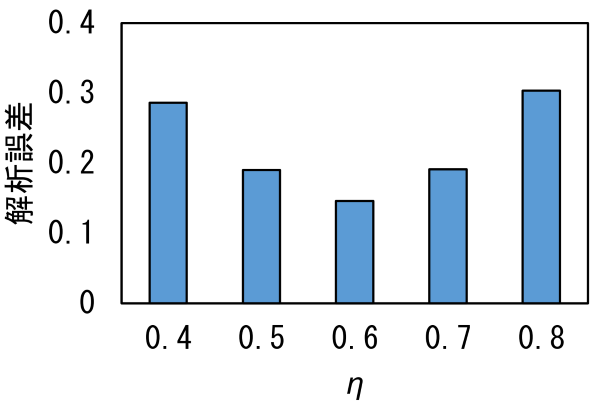
　解析の誤差δを、接点温度の実験値ΔT_T[K]と解析値ΔT_A[K]の差の総和をデータ数Dで除したものとした場合、図3のように係数η=0.6のときに最も誤差が小さくなりました。

　このη＝0.6という値について、次号では理論的な根拠をご紹介する予定です。また、電気的摩耗に影響を及ぼすジュール熱による温度上昇についても、今後電力ニュースでご紹介する予定です。

[参考文献]

• 1)山下、根本：架線—パンタグラフの機械的接触に起因する摩耗メカニズム、RRR、Vol. 81、No. 5、pp.46-51、2024
• 2)日本鉄道電気技術協会：鉄道と電気技術、Vol. 35、No. 9、p.56、2024

直流き電回路を用いた再エネ電力送電の可能性

　電力ニュース123号（2024年2月）等でお伝えしたように、「2050 年までに脱炭素社会（カーボンニュートラル）を実現」の目標に向けて、鉄道電力分野においても再生可能エネルギー（以降再エネ）の活用が不可欠と考えられます。しかし、太陽光発電や風力発電といった天候変動型の再エネを鉄道電力網に大量導入しようとしても、大きな電力需要場所とは離れているために再エネ電力の活用が難しくなる場合があります。鉄道側の再エネの発電量が過剰になり電力系統側に供給しようとしても、系統側と鉄道側を接続する送電線容量の制約、あるいは系統側の再エネも余剰が生じていることも考えられ、受け入れ困難となることも想定されます。

　そこで、鉄道側の再エネの発電電力を、き電回路を介して電力需要の大きい地域まで送電することにより再エネ活用効果を向上させることが、解決手段の一つとして考えられます。ここでは、直流き電回路を介して再エネ電力を電力需要場所に送電することに関する可能性について、検討した例を紹介します。

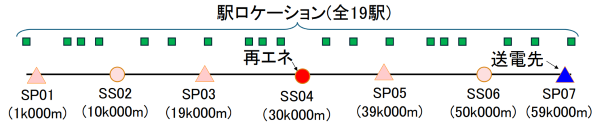
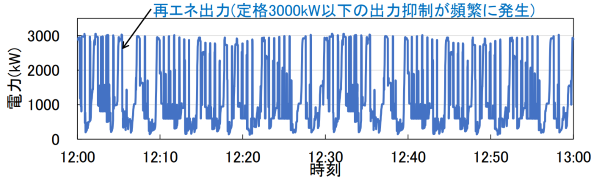
　路線モデルの概要を図1に示します。路線長60.0km、全線複線で変電所（SS、全て定格3000kW）がSS02、SS04、SS06の3箇所、き電区分所（SP）が4箇所ある架空の直流1500Vき電の郊外の線区（上下30分間隔で6両編成の電車が運行）をモデルとしました。再エネ（定格3000kW、ここでは12～13時の間で常に定格出力が可能）は、線区の中央にあたるSS04においてき電回路に連系する想定としました。送電先はSS04から29km離れたき電区分所であるSP07に設定しました。

　再エネ送電を実施しない（送電先がない）場合の再エネ出力電力の計算結果を図2に示します。再エネ電力3000kWをき電回路に出力させようとしても、閑散線区ゆえに力行負荷が存在しないタイミングにおいて再エネ出力が頻繁に抑制されます。その出力の平均は1200kW程度にとどまり、出力抑制により再エネ定格の半分を下回りました。

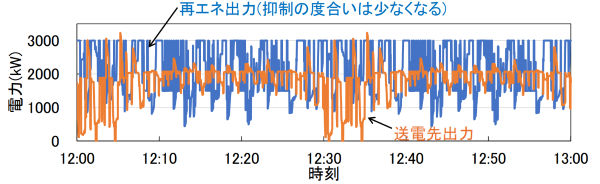
　次に、再エネ送電想定時における再エネと送電先の各出力電力の計算結果を図 3に示します。一部の時間帯（30分間隔）において送電先の出力が大きく低下します。これは送電先の付近において電車負荷が存在することで、き電電圧が極端に低下する影響を抑制するために、一時的に出力電流を抑制する必要が生じたためです。一方、再エネの出力の平均は2000kW強であり、図2と比較すると抑制の影響が軽減され、送電によって再エネ活用効果を高めることにつながりました。一方、送電先出力の平均は1800kW強となり、再エネ出力よりも若干下回りました。

　再エネ送電の直流き電システムへの適合性を評価するにあたり、他にも例えば電圧降下、設備の温度上昇、レール対地電圧の各影響を把握する必要があります。今後も、再エネ電力送電の可能性を多角的な視点で精査し、実現可能性のあるモデルを提案していきます。

【ワンポイント講座】大型低騒音風洞を活用したパンタグラフ揚力の測定

　パンタグラフが高速走行を行うと、部材各部に大きな空気力が作用して押上力が変化します。この、空気力による押上力の増分のことを「パンタグラフ揚力」と呼んでいます。パンタグラフ揚力は、大きすぎると架線にダメージを与えてしまう一方で、小さすぎると離線が頻発し、マイナスの値になると最悪の場合パンタグラフが折り畳んでしまう要因となります。そのため、パンタグラフが良好な集電性能を発揮するうえでは、パンタグラフ揚力を大きすぎず小さすぎず常に適正な値に維持することが重要です。パンタグラフ揚力には明確な基準値は存在しませんが、経験的には最高速度でおおよそ30N～60N程度の値になるように、舟体などの形状が選定されています。

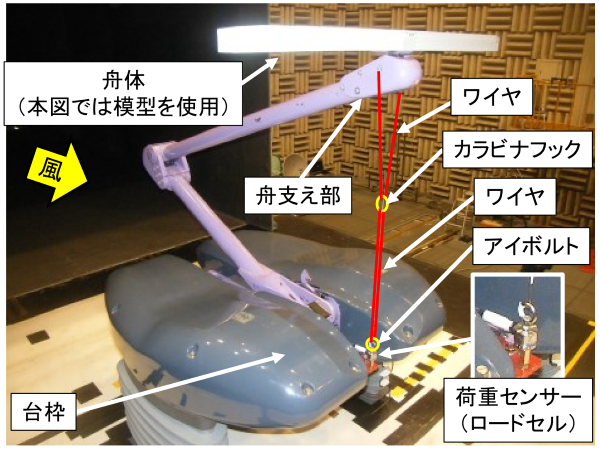
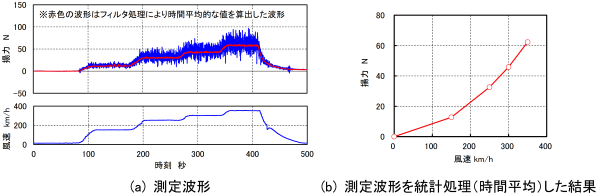
　パンタグラフ揚力は最終的には現車試験で測定・評価が行われますが、それ以前の開発段階では、多くの場合、鉄道総研が所有する大型低騒音風洞（図1、所在地：滋賀県米原市）において測定・評価が行われています。風洞とは定置で物体に風を当てて、様々な空力特性を測定・評価するための設備です。大型低騒音風洞（開放型測定部）は、吹き出し口寸法が3m×2.5mと大きく、最高風速400km/hでの送風が可能なことから、実機のパンタグラフを設置して現車と同じ風速で風洞試験を行うことが可能です。実際の風洞試験では、図2のように台枠（または地面板）に荷重センサー（ロードセル）を設置し、荷重センサーと舟支え部との間をワイヤ等で接続して作用高さを固定した状態で、無風時に対する送風時の荷重の増分を検出することでパンタグラフ揚力を測定します。図3はパンタグラフ揚力の測定例であり、風速が増加するにつれて揚力が大きくなる様子がわかります。

　このように、鉄道総研では大型低騒音風洞を活用したパンタグラフ揚力の測定・評価を行うとともに、パンタグラフ揚力の発生・変化メカニズムの解明やその安定化のための研究開発を行っています。