電力ニュース
2018年12月号
暴露した硬銅トロリ線の接触抵抗の推移
トロリ線しゅう動面に生成する腐食生成物や気動車による煤煙などの汚損物の付着によりトロリ線~すり板間の接触抵抗が増加し、ジュール熱やアークの発生に伴うトロリ線の軟化が生じ、最終的には架設張力によって破断に至る場合があります。ここでは、暴露した硬銅トロリ線の接触抵抗測定結果の一例をご紹介します(文献1)。
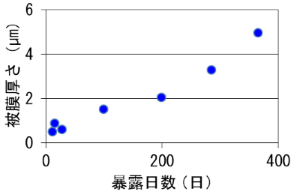
海岸(湾)から20m程度離れた沿岸部において、列車進入がない無効区間のトロリ線箇所に、硬銅トロリ線(摩耗していない新線)を1年間、直流1500Vで加圧暴露しました(図1)。暴露日数とトロリ線しゅう動面に生成する被膜厚さの関係を図2に示します。暴露試験を行った範囲では被膜厚さが増加傾向にあることがわかりました。
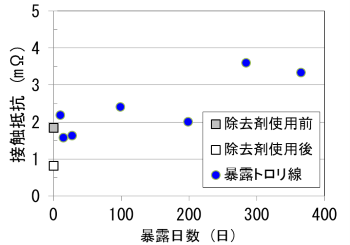
次に、鉄道総研の所有する直動摩耗試験機を用い、暴露したトロリ線と代表的な銅系焼結合金すり板(BC)の接触抵抗測定を行いました。なお、暴露試験開始前には、暴露するトロリ線を銅酸化被膜除去剤に30分間浸して被膜の除去を行いました。測定結果を図3に示します。被膜厚さの成長に伴い接触抵抗が増加傾向にあることが分かりました。また、被膜除去前後の接触抵抗測定結果も図3に示しますが、薬剤の使用に伴う被膜の除去により接触抵抗が半減すること、およそ1か月間以内の暴露では、薬剤を使用していないトロリ線と接触抵抗が変わらないことが分かります。
ここでご紹介した結果や、上記の暴露トロリ線や実際に使用していたトロリ線と実際のパンタグラフ(銅系すり板を搭載)を用いた接触電圧測定、シミュレーションソフトを用いた電車線とパンタグラフの温度上昇解析から、バッテリ電車への急速充電においてパンタグラフがしゅう動しないトロリ線におけるトロリ線保全周期の提案(文献2)を行いました。また、この結果を電留線などのパンタグラフのしゅう動頻度が少ないトロリ線のしゅう動面研磨周期の検討にも活用していきたいと考えています。
〔参考文献〕
- 臼木理倫ほか:トロリ線表面に生成する被膜と接触抵抗の関係, 平成27年電気学会産業応用部門大会, 5-21, pp.V-205~V-208, 2015
- 早坂高雅ほか:バッテリ電車の急速充電に対するトロリ線の保全周期の考察, JREA, 第59巻, 第12号, pp.15-18, 2016
がいしの等価塩分付着密度と鋼板腐食との相関の検討
鉄道電力設備において、腐食度評価用試験片の暴露試験により腐食度を調査し、その結果に基づいて腐食マップを作成した例はありますが、腐食マップを反映した設計・保守指標はありません。また、鉄道は敷設距離が長く、海岸沿いやトンネル等もあり環境の変化に富むため、全ての沿線環境で腐食度評価用試験片の暴露試験を行うためには、相当なコストが必要となります。
他方で、鉄道事業者には、電車線路設備を設計・保守するにあたっての、がいしの汚損度を考慮する指標、等価塩分付着密度(Equivalent Salt Deposit Density、以下ESDD、単位:mg/cm2)が存在します。そこで、この指標を活用し、がいし汚損度から鋼板の腐食度を推定する手法について検討を行っています。
推定手法を検討するために、延べ20日間の短期間のがいしと鋼板の暴露試験を行いました。試験の様子を図1に示します。鋼板は全て初日から暴露して、各日1枚ずつ回収しました。鋼板の腐食度は、初期質量に対する質量増加率で評価しました。また鋼板回収時にESDDの測定を行いました。
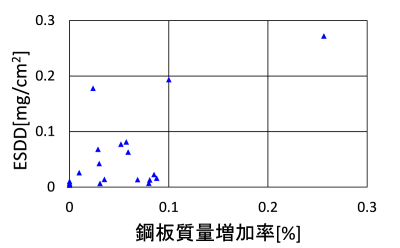
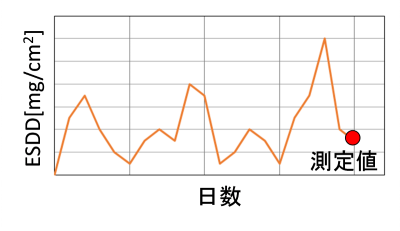
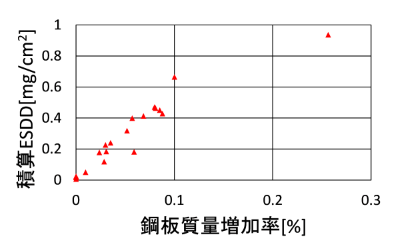
鋼板の質量増加率と、鋼板を取り外した日のESDDの関係を図2に示します。図中に示すように、両者の関係にはばらつきがあります。これは、腐食は不可逆な現象であるのに対し、図3に示すように、ESDDは海塩の飛来や降雨の影響により時々刻々変化するため、長期間が経過するほど、鋼板の腐食とその時点でのESDDとの相関が小さくなるためです。
そこでESDDを初日から鋼板を取り外した日まで積算したESDD(以下、積算ESDD)と、鋼板の質量増加率の関係を調べました。その結果を図4に示します。鋼板の質量増加率と積算ESDDの相関係数 R は 0.94 でした。このように、1回のみ測定したESDDではなく、複数回測定したESDDを積算した値を用いた方が、鋼板の腐食度を精度よく推定できることを確認しました。今後は、ESDDの測定周期と腐食度の関係を検討するため、中長期の暴露試験を行う予定です。
HILSによるパンタグラフ接触力制御手法の評価試験
鉄道の高速化を実現するために、架線とパンタグラフ間に生じる接触力変動を低減する技術が求められています。このような接触力変動の低減手法として、鉄道総研ではアクティブ制御機構を備えたパンタグラフを開発しています。
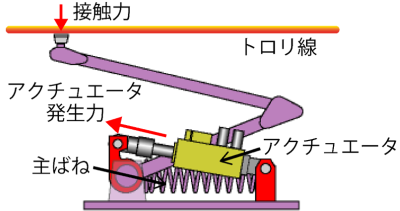
本パンタグラフは、図1に示すように主ばねと並列に空気圧アクチュエータを設け、アクチュエータ内の空気圧を調整することでパンタグラフの押上力をアクティブに制御します。現在開発中の手法では、接触力変動のうち、パンタグラフが支持点を通過する周期に起因した径間周波数とその2倍の周波数成分を制御対象とします。そこで、列車速度と支持点間隔に基づいて径間周波数を算出し、これを既知情報としたフィードフォワード制御を行います。さらに、測定された接触力をフィードバックし、制御ゲインと位相を適応的に自動調整することで、より効果的に接触力変動を低減します。
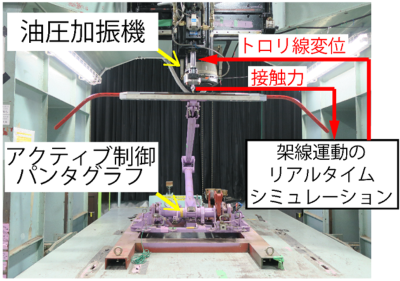
本手法の効果を検証するために、架線運動のリアルタイムシミュレーションと実機アクティブ制御パンタグラフとを組み合わせたHILS試験を実施しました。本HILS試験では、図2に示すように油圧加振機を用いて実機パンタグラフを定置で加振し、パンタグラフの接触力に基づいて計算されたトロリ線の変位を加振機が実現することにより、パンタグラフが実架線下を走行している状況を再現することができます。これにより、従来用いられていた強制変位加振に基づく検証試験よりも実際の走行状況に近い環境下で制御手法を検証することができます。
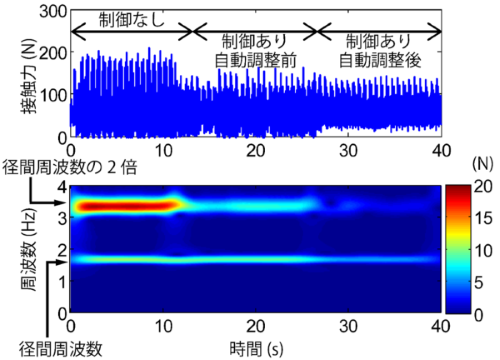
本試験ではパンタグラフが走行速度 300km/h で新幹線用シンプル架線下を走行する状況を模擬しました。架線モデルは径間長が 50m で一定とし、このときの径間周波数は 1.6Hz です。図3に、HILS試験で得られた接触力の時刻歴波形と、その時間-周波数解析結果を示します。制御なしの状態に対して、制御ゲイン・位相の自動調整を行わずに制御した状態では接触力変動が低減されているものの、依然として離線(接触力がゼロの状態)が多発しています。これに対し、制御ゲイン・位相を自動調整することで、自動調整前よりも接触力変動が低減され、離線の発生を抑制することができました。
今後は、径間長や列車速度が可変である場合のHILS試験を実施することで、本制御手法のさらなる改良と検証を行います。
耐震設計における門形柱の線路方向の固有周期
電車線路設備耐震設計指針(以下、耐震指針)では、まくらぎ方向(線路直角方向)に加えて線路方向(線路平行方向)の振動について、主に電化柱の曲げ変形に対する耐力を評価しています。その際、鉄道構造物(盛土や高架橋等)と電化柱との共振現象を考慮して、それぞれの固有周期を求めて耐震指針の加速度応答スペクトルから地震時に作用する応答加速度を算定しています。しかしながら、現在の評価手法では、電車線等の架設の影響を考慮して電化柱の固有周期を求める手順にはなっていません。
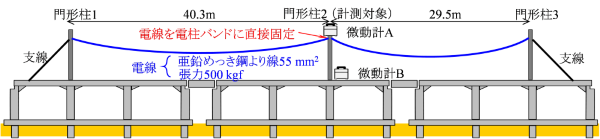
電化柱の固有周期については、1本の電化柱で電車線などを支持する構造の単独柱では、振動方向によって固有周期が大きく変わることはほとんどありません。一方、門形柱は2本の電化柱をビームで結合する構造により、門形柱全体系としての剛性はまくらぎ方向で増加しますが、線路方向に対する剛性は増加しないため、一般的に門形柱ではまくらぎ方向と比較して線路方向の固有周期が長くなります。同一の鉄道構造物上に建植された電化柱はその固有周期が長くなると、地震時の応答加速度が大きくなる傾向があります。このため、鉄道構造物上の門形柱は、まくらぎ方向と比較して線路方向の応答加速度が大きくなることが予想されます。その一方、実際の地震被害では門形柱が線路方向に倒壊する事例はほとんど見られず、現状の手順による評価と食い違う場合があります。そこで、電車線等の架設が門形柱の固有周期へ与える影響について、図1に示す条件で実設備の微動を計測することによって確認しました。
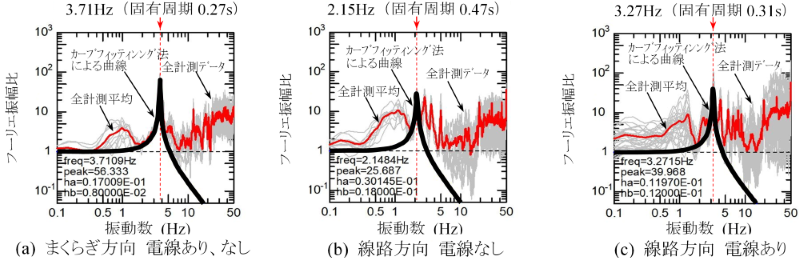
微動計測の結果を図2に示します。図2は、微動計Aと微動計Bの計測波形から伝達関数を得て、門形柱2の1次モードの固有周期を求めたものです。その結果、門形柱の固有周期は、架設電線の有無に対してまくらぎ方向では変化せず(図2(a))、線路方向では架設電線なしと比較して架設電線ありの条件で固有周期が短くなり(図2(b)、図2(c))、方向別の固有周期の差が小さくなることを確認しました。今後は、架設する電車線等の線種や張力、固定の構造などの条件に対して、門形柱の線路方向の固有周期がどの程度変化するかを確認し、その結果を門形柱の耐震性能評価に適用する予定です。
【ワンポイント講座】有限要素法(FEM: Finite Element Method)
コンピュータ技術の発達に伴い、多くの場面でコンピュータシミュレーションが利用されています。シミュレーションには様々な種類がありますが、構造物の変形などを計算する手法として有限要素法が広く使用されており、鉄道総研の電力部門では現在開発中の架線/パンタグラフシミュレータで使用しています。本稿では静的な荷重が作用する部材の変形を例に有限要素法を概説します。
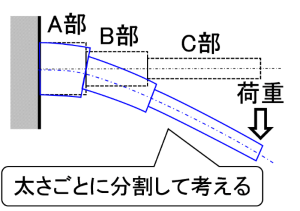
部材に荷重が作用したときの変形量を計算するとき、材料力学では構造物をある程度の大きさを持つかたまり、もしくはそれらの集合体として扱います。例えば、図1のように、太さが段階的に変化する梁(はり)の変形を求めるとき、太さごとに分割(A部~C部)して、各部材の変形を求めて足し合わせることで全体の変形を求めます。本例のような単純な形状の構造物であれば容易に変形量を求められますが、複雑な形状の構造物の変形などを計算することは一般的には困難です。
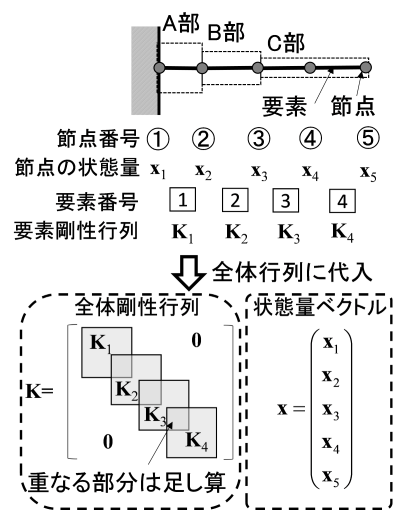
有限要素法では、前述の例と同様に対象とする構造物を「有限」の数の「要素」の集合体とみなします。さらに要素端部などに「節点」を設け、節点の変位により要素内の変位分布を近似することによって、構造物全体の変形を求めます。はじめに、構造物を有限の数の要素に分割します(図2の 1 ~ 4 )。その後、構造物全体の剛性(硬さ)を表す行列 K(全体剛性行列)と節点の変位を表すベクトル x(状態量ベクトル)の積が、各節点に作用する力を表すベクトル F(荷重ベクトル)と等しいという式(Kx = F)を解くことで全体の変形量を求めます。このように構造物を分割して各要素の特性を全体剛性行列に組み込むことで、複雑な形状に対しても容易に計算を行うことができます。
有限要素法による計算例として電車線の静構造計算結果を図3に示します(文献1)。この計算では、トロリ線やちょう架線に張力や重力が作用していること、ちょう架線は支持点で固定されていること、などの条件を与えています。このように、有限要素法を用いることで電車線のような複雑な構造物の計算を行うことができます。
本稿では有限要素法の概説をしました。実際はもっと複雑な理論により有限要素法は構成されています。詳細については多くの専門書がありますのでご覧いただければ幸いです(例えば、文献2)。
〔参考文献〕
- 小山達弥, 池田充: 3次元構造に対応した架線・パンタグラフ運動シミュレーション, RRR, 2015
- 栗﨑彰: 図解 設計技術者のための有限要素法はじめの一歩, 講談社, 2012