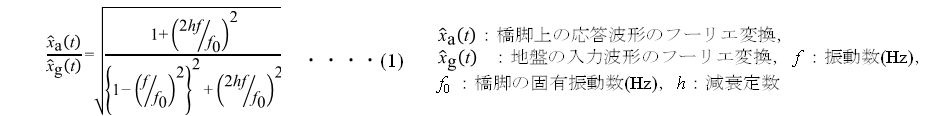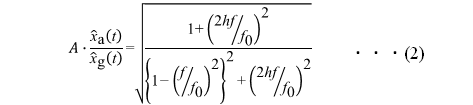施設研究ニュース

• PDF版はこちら

• 同一構造区間で生じる保守多投入箇所の軌道沈下の再現試験
• 低圧縮量レールガス圧接工法の開発
• 常時微動による橋脚固有振動数の推定精度向上手法
• 耐震設計における慣性力と地盤変位の組合せの改良

同一構造区間で生じる保守多投入箇所の軌道沈下の再現試験

１．はじめに

　バラスト軌道では，列車の繰返し荷重によってまくらぎ下のバラスト粒子が移動することでまくらぎが沈下し，高低変位が生じます．そのため，定期的な軌道検測が行われており，高低変位の大きい箇所に対しては，つき固め作業が行われています．つき固め作業では，軌道をこう上してレールレベルを整正し，こう上したことで生じるまくらぎ下の隙間に，タイタンパと呼ばれる保守専用の振動機械でバラストをつき込みます．このようにバラスト軌道は列車荷重による沈下の発生を前提とした構造ですが，つき固め作業により簡易に軌道整正しやすい特徴を有します．
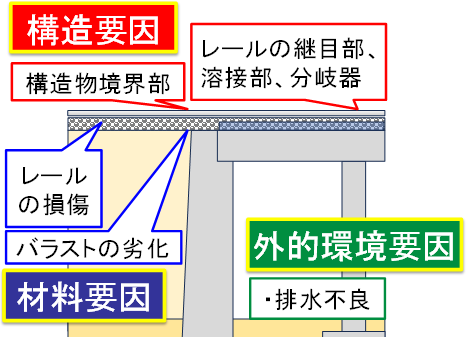
　バラスト軌道の高低変位は同一箇所で繰り返し生じやすいですが，この主な要因として，構造物境界部などの構造的な要因，バラスト劣化などの材料的な要因および地下水位が高いといった外的環境要因が考えられます（図1）．一方で，このような条件に該当しない区間においても，特別な原因がないものの，つき固め作業後に同じ位置で高低変位が大きくなる現象がしばしば確認されています．海外においても，バラストの沈下の分布形状が元に戻る現象が確認されており，”Ballast Memory”と称されています¹⁾（以降，バラストメモリとします）．
　本研究では，バラストメモリのメカニズム解明の一環として，軌道検測データよりバラストメモリの発生要因を分析し，小型模型を用いたバラストメモリの再現試験を実施して，バラストメモリが生じる原因に関する基礎検討を行いました．

２．構造物の応答変位の算出方法

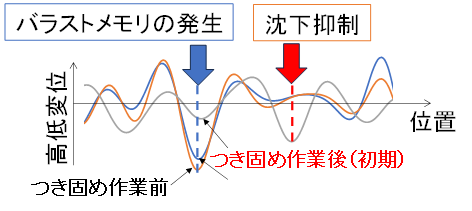
　軌道検測データを用いて，つき固め作業前後の高低変位波形の経時変化からバラストメモリに該当する箇所を抽出し，発生要因を分析しました．バラストメモリのデータ抽出条件は，ロングレール区間を対象とし，高低変位が発生しやすい分岐器区間，伸縮継目（EJ）区間，接着絶縁継目（IJ）区間，道床交換の前後4m未満の区間，構造物境界部の前後10ｍ未満の区間，レール溶接部の前後2m未満の区間を除外しました．また，バラストの劣化の影響を排除するために，道床交換から5年以内にバラスト交換を実施した箇所を対象としました．さらに，つき固め作業前後の高低変位を比較して同一箇所で3mmより大きな高低変位が2回以上生じ，つき固め作業前に最大の高低変位が発生した箇所と同じ位置で沈下が再発した場合を，バラストメモリの発生箇所と判断しました（図2）．

　調査した軌道延長980kmのうち，上記の条件で抽出した区間は合計96.3kmであり，そのうち388箇所でバラストメモリが発生していました．定期的に実施するマルチプルタイタンパ（以下，MTT）によるつき固め作業，およびそれ以外に必要に応じて実施するハンドタイタンパ（以下，HTT）によるつき固め作業についてバラストメモリの発生状況を分析しました．また，MTTにおいては，軌道状態に関わらず，年1回の頻度で施工する箇所もあることから，ここでは，つき固め作業から1年後の高低変位が3mm未満を「沈下抑制」，3mm以上を「再沈下」と判定しました．
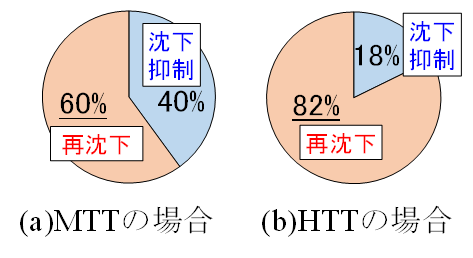
　図3にMTTおよびHTTのつき固め作業後の沈下抑制と再沈下の割合を示します．つき固め作業から1年後の時点で，沈下が再発した割合は，MTTで6割以上，HTTでは8割以上でした．ここで，つき固め作業前の軌道のこう上量の平均値は，MTTが4.1mmに対して，HTTの方が大きく5.2mmでした．また，再発割合がMTTとHTTで異なり，HTTの方が高くなった要因として，MTTの場合は平均的に軌道状態が悪い区間を定期的に施工しているのに対して，HTTでは保守多投入箇所に対して実施していることが影響したと考えられます．以上より，つき固め作業前の軌道のこう上量が，バラストメモリの発生に影響を及ぼすと考えられました．

３．小型模型を用いたバラストメモリの再現試験

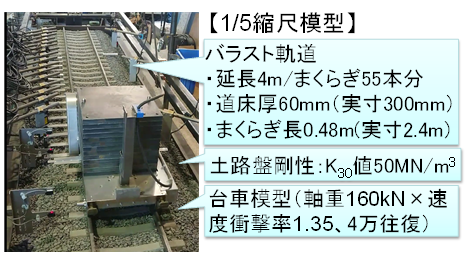
　前章の実態調査を踏まえ，小型模型を用いた移動載荷試験により，つき固め作業に着目したバラストメモリの再現試験を行いました（図4）．軌道模型の縮尺は1/5とし，相似則を考慮した模型条件としました．軌道模型の延長は4.0mとし，土構造物上における標準軌のバラスト軌道（道床厚60mm）を模擬しました．路盤模型は，地盤反力係数K₃₀値=50 MN/m³の一様な土路盤と同程度の剛性となるように，FEM解析により層構成を設定しました．

　輪重864N（軸重160kN×列車速度285km/hの速度衝撃率1.35 ²⁾の1/5縮尺相当）を模型レールに作用させるため，4輪の台車模型の質量を350kg程度とし，軸距は500mmとしました．載荷回数は4万往復とし，軌道模型中央の2.0m区間（まくらぎNo.1～No.18）を速度500mm/sで自走により定速走行させました．試験手順は，まず，4万往復走行の予備載荷で軌道を沈下させた後に，精緻に機構を再現したMTT模型を用いたつき固め作業を実施し，軌道を整正しました．次に，4万往復走行の載荷試験とつき固め作業を2回繰り返しました．つき固め作業は，最も沈下していないまくらぎ位置を基準にして軌道全体を1mmこう上させました．従って，沈下量が大きい箇所ほどこう上量が大きくなります．つき固め作業は，つき固め位置・手順・時間を全セットとも同じ条件としました．
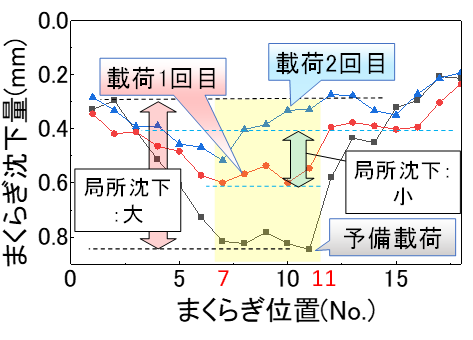
　図5に定速走行区間における4万回走行後のまくらぎ沈下量の分布を示します．予備載荷では，まくらぎNo.7～No.11に対して，MTT模型によるスクイズを実施せずにツールの挿入のみ行うことで，局所的なバラストの沈下を再現しました．載荷1回目では，予備載荷で局所的な沈下を再現したまくらぎNo.7～No.11において，局所的な沈下が再発しました．載荷2回目では，まくらぎNo.7～No.11の沈下量が前後の区間と比較して同程度以下になり，沈下量が最大となる位置が変化しました．以上より，局所的な沈下が大きくてこう上量がある程度大きいと沈下が再発し，局所的な沈下が小さくてこう上量も小さいと，つき固め作業による沈下の再発が抑制されると考えられます．

４．おわりに

　軌道検測データと保守履歴からつき固め作業がバラストメモリの発生に影響していることを示しました．また，小型模型を用いたバラストメモリの再現試験により，同一構造で生じる沈下の再発には，つき固め作業前の局所的な沈下量と軌道整正時のこう上量が影響を及ぼすことを示しました．

【参考文献】

1）Earnest T.Selig and John M.Waters：Track Geotechnology and Substructure Management,1994.
2）中村貴久，廣尾智彰：同一構造区間で生じる保守多投入箇所の軌道沈下の再現試験，第79回年次学術講演会，土木学会，Ⅵ-1311，2024.

執筆者：軌道技術研究部 軌道・路盤研究室 中村貴久
担当者：軌道技術研究部 軌道・路盤研究室 廣尾智彰

低圧縮量レールガス圧接工法の開発

１．はじめに

　レールガス圧接法はレール同士をつき合わせガス炎により加熱しながら加圧することにより接合するレール溶接法の一種で，他のレール溶接法に比べて信頼性の高さと使用機材の機動性の高さを両立していることが特徴です．
　一方で，現行のレールガス圧接法では一般的に接合強度を確保するため圧縮量を24mm以上としており，圧接時の塑性変形により生じるふくらみ（以降余盛とします）を専用の機材を用いて圧接直後に押抜く作業（図1）を必要とします．本研究では，機材の軽量化や作業工程の簡略化を目的とした新たなレールガス圧接工法として，余盛の押抜きを必要としない低圧縮量のレールガス圧接工法を提案し，新工法によるレールガス圧接部の曲げ性能評価を行いましたので，ご紹介いたします．

２．変圧法を用いた低圧縮量レールガス圧接部の作製

　圧縮量を減少させても現行と同様の接合強度を維持するため，本研究では過去に継手性能の向上が示唆された圧接中のレールへの加圧力を変化させる変圧法¹⁾に着目し，JIS60kg普通レールを用いて低圧縮量のレールガス圧接部を作製しました．
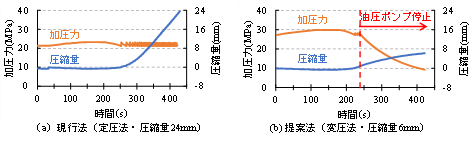
　図2に加圧力一定の現行法（定圧法）と提案法（変圧法）で作製した際に測定した圧縮量と加圧力の関係を示します．現行の定圧法ではレールに対し一定となる22MPaの加圧力を載荷し，圧縮量24mmに到達するまで加熱および加圧するのに対し，提案の変圧法では最初により高い28MPaの加圧力を載荷し，圧縮量1mmに到達後油圧ポンプを停止することで，シリンダーやホース内の残圧により徐々に加圧力を低下させ，現行法の標準的な加熱時間である420秒経過後に圧接を終了しました．こうすることで，レールに対する入熱量を十分に確保しつつ圧縮量を約6mmとしたレールガス圧接部を作製しました．

　図3に現行法の圧縮量24mmで押抜き後の圧接部と提案法の圧縮量約6mmで押抜き無しの圧接部の仕上げ研削前の外観を，表1にぞれぞれの圧接部のグラインダーによる仕上げ研削時間の例を示します．提案法は，現行法の押抜き後に比べて長手方向の余盛幅が狭く，ほぼ同等もしくはそれ以下の研削時間であることから，仕上げ研削作業の負担量はほぼ変わらないと言えます．

３．静的曲げ試験

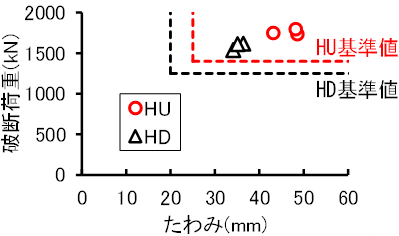
　レールガス圧接部の静的な曲げ強度を評価するため，提案法で作製したガス圧接部に対し，支点間距離1m，中央集中荷重による静的曲げ試験を実施しました．破断姿勢を頭部上向き（HU）および頭部下向き（HD）としてそれぞれ3体ずつガス圧接部を破断させ，破断時の荷重-たわみ値をまとめたグラフを図4に示します．すべてのガス圧接部がJIS60kg普通レールガス圧接部の破断時の荷重-たわみ値の基準値（HU：1400kN-25mm，HD：1250kN-20mm）を満たし，十分な曲げ強度を有していると言えます．

４．曲げ疲労試験

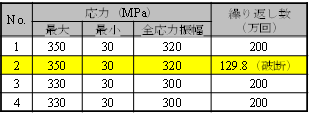
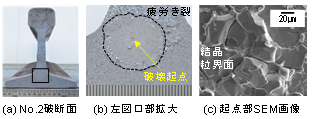
　繰り返しの列車荷重による影響を評価するため，通常の列車荷重負荷方向と同様のHU姿勢にて4点曲げ疲労試験（支点間距離1300mm）を実施しました．表2に曲げ疲労試験結果を示します．同様の条件で現行法のレールガス圧接部の繰り返し数200万回の曲げ疲労強度は320MPaと言われています²⁾が，同等の全応力振幅320MPaの片振り条件下ではガス圧接部2体中1体（No. 2）が約130万回の繰り返し数で破断するという結果になりました．

　図5にこの破断面および起点部を示します．破断面下首部に円形の疲労き裂が認められ，その破壊起点を走査型電子顕微鏡（SEM）で観察すると，図５(c)に示すように結晶粒界で割れている様子が観察されました．通常のレールガス圧接部に比べ加圧力，圧縮量が小さい提案法ではこのような割れが圧縮されることなく残存してしまったと考えられますが，欠陥のサイズは直径1mm程度であり，レール溶接部の超音波探傷試験で不良判定となる欠陥サイズに対して極めて小さい³⁾ため，実用上疲労破壊の起点にはなり得ないと思われます．また全応力振幅300MPaとしたガス圧接部2体は200万回の繰り返し載荷を達成したことから，提案法による低圧縮量レールガス圧接部は最大約280MPaと言われるエンクローズアーク溶接部²⁾以上の曲げ疲労強度を有していると言えます．

５．まとめ

　加圧力を変化させる変圧法の採用により，列車荷重に十分に耐えうる強度を有する余盛の押抜き作業が不要な圧縮量約6mmのレールガス圧接部の作製が可能であることが分かりました．今後今回提案した工法による現場施工試験等を行い，実用化に向けた検討を引き続き進めていく予定です．

【参考文献】

1)　深田康人，辰巳光正，山本隆一，上山且芳：レールガス圧接部の信頼性向上に関する検討，溶接学会論文集，21巻1号，pp. 39-45，2003
2)　新版軌道材料編集委員会：新版軌道材料，p. 119，鉄道現業社，2011
3)　辰巳光正，上山且芳，山本隆一，工藤松一：レール溶融溶接部折損防止のための超音波探傷検査，鉄道総研報告，9巻12号，pp. 43-48，1995

執筆者：軌道技術研究部　レールメンテナンス研究室　小納谷優希
担当者：軌道技術研究部　レールメンテナンス研究室　伊藤太初

常時微動による橋脚固有振動数の推定精度向上手法

１．はじめに

　豪雨時の河川増水により橋脚周囲が洗掘を受け，最終的に傾斜や沈下などの災害に至る場合があります．筆者らは鉄道橋脚を対象とした常時微動計測に基づく固有振動数の状態監視手法を開発してきました¹⁾．本稿では，固有振動数を推定する演算処理（以下，推定アルゴリズムという）を改良して推定精度を向上する手法と，洗掘を模擬した大型模型実験の結果を用いて検証した結果について述べます．

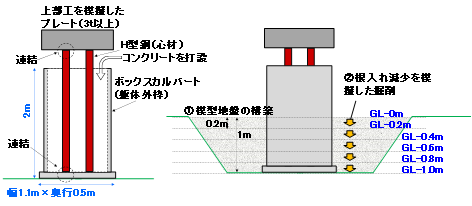
２．実験概要

　橋脚模型および模型地盤の状況を図1に示します．橋脚模型は実物の1/3縮尺であり，幅1100mm，奥行き740mm，高さ1995mmの直接基礎形式です．根入れの初期条件は基礎底面より1mであり，200mmずつ段階的に掘削して洗掘の進行性を模擬します．模型地盤の地盤材料は稲城砂（ρ_dmax＝1.765g/cm³），目標締固め度90%です．各掘削段階において，開発段階で利用した速度センサと，より安価な加速度センサを用いて常時微動の同時計測を行い，固有振動数の推定精度を比較しました^2),3)．使用した微動計および設置状況を図2に，常時微動計測における計測条件および計測データ数を表1に示します．

３．固有振動数推定アルゴリズム

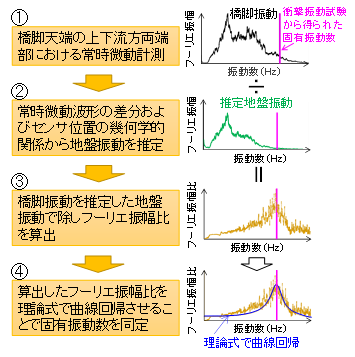
　詳細は文献1)に記載のとおりですが，推定アルゴリズムは橋脚天端両端部で計測された微動波形から橋脚ロッキング振動に相当する応答波形と入力波形をそれぞれ算出してフーリエスペクトルを求め，両者の比（伝達関数）で表されるフーリエ振幅比に式(1)で示す理論解をフィッティングして固有振動数を推定するものです（図3）．

４．加速度波形の振動特性と推定アルゴリズムの改良

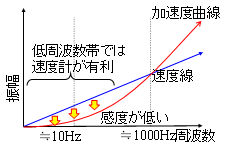
　表１で示したデータを対象に加速度計計測データの振動特性について整理します．加速度センサの特性として，低周波数帯では速度センサよりも低感度であることが挙げられます（図４）．計測した加速度波形に対して改良前の推定アルゴリズムを適用すると，固有振動数の低下傾向はGL-0.6m程度までは評価可能なものの，全体を通じて衝撃振動試験による固有振動数と一致する結果を得ることができませんでした．その理由についてフーリエ振幅比の形状から考察します．
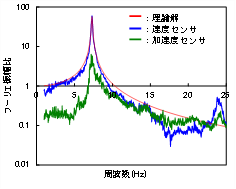
　図5は，推定アルゴリズムを適用して得られたフーリエ振幅比のうち，明示的な速度計および加速度計の特徴を示した例です．速度センサによるフーリエ振幅比は卓越振動数が明瞭で，周波数帯全体では外部ノイズとみられる振動も少なく振動理論解とよく一致します．それに比べ，加速度センサによるフーリエ振幅比はいずれも振幅が速度センサよりも1オーダー程度小さくなっています．これは，上述のとおり低周波数帯の感度が低いためロッキング振動成分が分離できず入力波形を過大に推定している可能性などが理由として考えられます．一方、振幅比は小さいものの速度波形で得られたフーリエ振幅比と相似形を呈しており，同様の特性を有する計測波形が多数存在することが分かりました．
　そこで，新たな演算処理を追加し固有振動数の推定が可能となるよう推定アルゴリズムを改良しました．改良点として，従来のフィッティング時の変数が固有振動数と減衰定数の二変数であったものに対し，新たにフーリエ振幅比の増幅率Aを設け式(1)の左辺に乗じる形で追加しています．

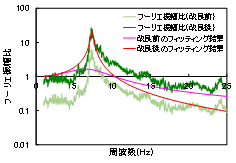
　この処理により，低周波数帯の感度が低い加速度計で得られたデータである固有振動数付近にフーリエ振幅比のピークが存在するもののフーリエ振幅比が著しく小さく推定不能となる波形に対し，その波形を増幅することで理論解にフィッティングすることが可能となります．図6は改良前後のフィッティング結果の一例を示したものです．上記の改良により，フーリエ振幅比が固有振動数付近に明瞭なピークを示しているのにも関わらず，理論解で十分なフィッティングが出来ないものを補完し，推定精度を向上させることが可能となっています．

５．まとめと今後の展望

　本手法を実装した微動計測システムにより，今後もデータの蓄積を図るとともに適用条件の明確化を図りたいと考えています．なお，本手法は衝撃振動試験IMPACTUSの一部機能として実装する予定です．

参考文献

1) 欅健典，湯浅友輝，内藤直人，渡邉諭：橋脚天端両端部の微動計測による橋脚基礎地盤の洗掘に対する健全度評価手法，地盤工学ジャーナル，Vol.13，No.4，pp.319-327，2018
2) 入栄貴，渡邉諭，藤原将真：橋脚基礎底面の洗掘進行に伴う基礎の安定性の変化に関する実験的検討，第56回地盤工学会研究発表会，12-8-1-07，2021
3) 藤原将真，渡邉諭，入栄貴：基礎底面の洗掘進行に伴う直接基礎橋脚の傾斜挙動の把握のための模型実験，第56回地盤工学会研究発表会，12-8-1-06，2021

【謝辞】本研究は，国土交通省の交通運輸技術開発推進制度（JPJ002223）の助成を受けたものです．
執筆者：防災技術研究部　地盤防災研究室　渡邉諭
担当者：防災技術研究部　地盤防災研究室　藤原将真，鈴木亜季，小原慶吾

耐震設計における慣性力と地盤変位の組合せの改良

１．はじめに

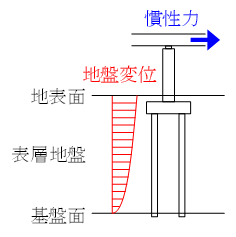
　深く根入れされた杭基礎などの基礎構造物は，地震時の慣性力だけでなく，地盤変位の影響も受けます（図1）．この慣性力と地盤変位の影響は必ずしも同時に最大となるわけではなく，時々刻々と変化しますが，耐震設計における作用としては基礎の応力や変形が最も厳しくなる瞬間を考慮すればよいことになります．そのため，耐震設計に用いる慣性力と地盤変位の組合せを適切に設定することが重要です．この組合せ係数を高い精度で推定できれば，構造物断面の合理化に繋がります．今回，組合せ係数の算定に用いるパラメータとして新たに地盤の特性を追加することで，慣性力と地盤変位の組合せ係数（以下，補正係数ν）の簡易算定式を改良する手法を提案した¹⁾ので紹介します．

２．地震作用の設定方法

　前述のように，耐震設計における地震作用には上部工からの慣性力と地盤変位があります．鉄道構造物の耐震設計では，地震作用は，①慣性力が最大になる瞬間，②地盤変位が最大になる瞬間を想定して設定しています²⁾．具体的には，式(1)，式(2)によって設定します．

①慣性力を中心とした設計	Rt = 1.0×Ra + ν ×f(z)	(1)
②地盤変位を中心とした設計	Rt = ν × Ra + 1.0 × f(z)	(2)

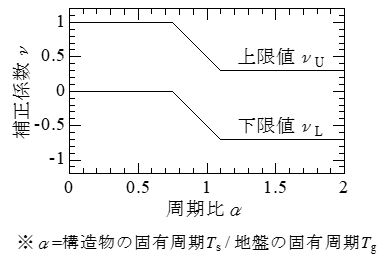
　ここに，ν：慣性力と地盤変位を組み合わせるための補正係数，R_t：考慮する地震作用，R_a：慣性力，f(z)：地盤変位です．この補正係数νの一例として図2が示されており，図2のように構造物の固有周期T_sと地盤の固有周期T_gの比率αによって使い分ける方法が採用されています．

３．地盤の固有周期が補正係数νに及ぼす影響

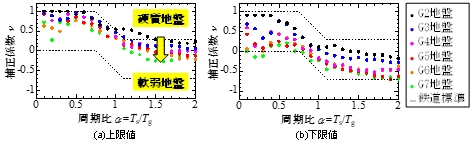
　補正係数νの傾向を把握するために，多様な地盤，構造物を対象に線形動的解析を実施し，その結果から補正係数νを整理しました．この補正係数νを地盤種別²⁾，地盤と構造物の周期比αごとに平均値を算し，地盤種別ごとに色分けした結果を図3に示します．図3から，上限値，下限値ともに軟弱地盤ほど，補正係数νが小さくなる傾向が確認できました．

４．提案する補正係数νの簡易算定式の概要

　今回，軟弱地盤ほど補正係数νが小さくなる傾向を図2の簡易算定式に反映させる方法を提案しました¹⁾．具体的には，式(3)，式(4)で補正係数νを算定することにより，鉄道標準²⁾による簡易算定式を，地盤の固有周期T_gに応じて増減させます．

(A) 上限値νUの算定	νU = 1.0 - 0.2Tg	( α ≦0.75 )	(3)
	νU = - 0.2α + 2.5 - 0.2Tg	( 0.75 < α ≦1.10 )
	νU = 0.3 - 0.2Tg	( 1.10 < α )
(B) 下限値νLの算定	νL = 0.3 - 0.2Tg	( α ≦0.75 )	(4)
	νU = - 0.2α + 2.5 - 0.Tg	( 0.75 < α ≦1.10 )
	νU = 0.3 - 0.2Tg	( 1.10 < α )

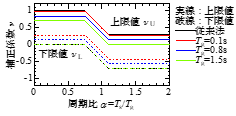
　地盤の固有周期T_gが0.1, 0.8, 1.5秒の時に着目して式(3)，式(4)を図示する（図4）と，硬質地盤（T_g = 0.1秒）よりも軟弱地盤（T_g = 1.5秒）の方が補正係数νが小さく，図3で確認した傾向を表現できています．なお，この提案式を用いることで，従来法（鉄道標準）に比べて補正係数νの算定精度が向上することも別途確認しています．

５．おわりに

　構造物の耐震設計における作用の組合せ係数の簡易算定式を改良した提案法を紹介しました．提案法を用いることで，地震作用が高精度化され構造物断面の合理化が期待されます．現在，地盤と構造物の非線形の影響を考慮した補正係数νの高度化³⁾，地盤，構造物の減衰の変化に伴う補正係数νの変化についても検討を行っています．今後，さらにほかの要素にも着目した検討を実施するとともに，これらを統合することで現状とほぼ同等の作業量でより適切な作用の組合せ係数の算定手法の提案を行います．

参考文献

1)　田中仁規，坂井公俊：鉄道の耐震設計における慣性力と地盤変位の組合せ係数の改良，土木学会論文集，Vol. 80, No. 13, 23-13119, 2024.
2)　鉄道総合技術研究所編：鉄道構造物等設計標準・同解説　耐震設計，丸善出版，2012.
3)　田中仁規，坂井公俊：地盤と構造物の非線形化を考慮した応答変位法における作用の組合せ係数の改良，日本地震工学会論文集，2024.

執筆者：鉄道地震工学研究センター　地震応答制御研究室　田中仁規
担当者：鉄道地震工学研究センター　地震応答制御研究室　坂井公俊

発行者：後藤　恵一　【(公財) 鉄道総合技術研究所　施設研究ニュース編集委員会　委員長】
編集者：北川　晴之　【(公財) 鉄道総合技術研究所　鉄道力学研究部　研究員】