施設研究ニュース

• PDF版はこちら

• 車上計測による支承あおり検知方法
• 都市部掘削工事における地盤改良体による盤ぶくれ対策工
• 多変量解析手法を用いた線区特性の評価手法

車上計測による支承あおり検知方法

1．はじめに

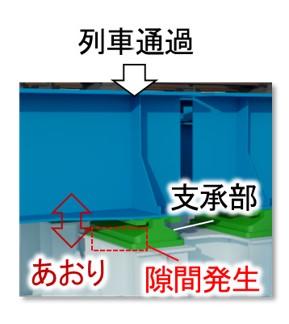
　鋼鉄道橋では，支点部に隙間が生じ列車通過時に支点部にばたつきが生じる支承あおり¹⁾が発生することがあります（図1）．支承あおりは疲労き裂などにつながるため，これまで技術者が定期的に現地に赴き，１橋りょうずつ目視で支承あおりの有無を判定しており，この検査に膨大な人工を要していました．このため，車上計測された軌道高低変位（以下，単に軌道変位と呼称）を用いて，支承あおり箇所を抽出し，検査箇所の絞込みができれば，大幅な作業の省力化が期待できます．一方で，車上計測された軌道変位から支承あおりの影響を抽出することは困難であり，その手法は実現されていませんでした．今回，数値解析での検討結果を基に，限られた条件ではあるものの，軌道変位の振幅を検知指標とした支承あおり箇所の抽出手法を開発しましたので紹介します．

2．支承あおりと軌道変位の関係

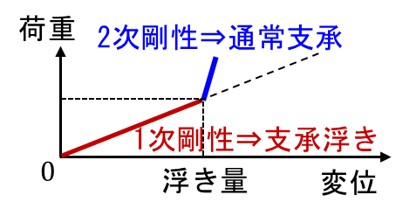
　まず数値解析により，これまでに未解明であった支承あおりと軌道変位との関係を検討しました．橋りょう・支承・レール・軌道締結装置を梁・ばねの有限要素でモデル化し，列車荷重を移動させる準静的な解析を行いました²⁾．図2に，支承あおりのモデル化を示します．１つの折れ点をもつ非線形ばねとしてモデル化しました．図中に示す「浮き」は，支承あおりが発生している支点部の隙間のことを指します．この非線形ばねは，浮きがある場合は支承の鉛直剛性が小さく（1次剛性），列車通過により浮きがつぶれると浮きのない通常の支承と同じ鉛直剛性（2次剛性）に変化する特性を持ちます．
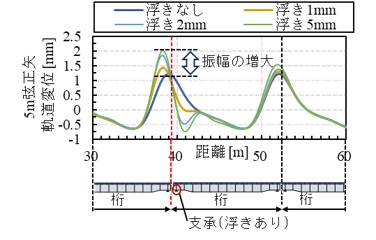
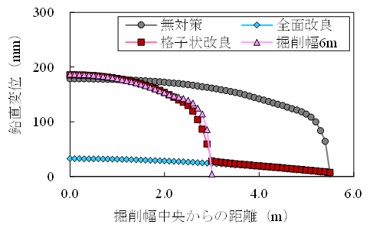
　図3に，数値解析で得られた軌道変位（5m弦正矢軌道変位）の結果を示します．数値解析では，桁が連続する区間のうち1箇所の支承に，1mm，2mm，5mmの浮き（支承あおり）を非線形ばねとして入力しています．同図より，浮きが大きくなるにつれて，浮きが存在する支点部での軌道変位振幅が局所的に増大することがわかります．

3．実路線での軌道変位の検証

　数値解析で得られた軌道変位の特徴について，実路線で検証を行いました．なお，実用に際しては，静的軌道変位と呼ばれるレールの凹凸やゆがみといった成分を除去する必要があります．図4に，手押し式の簡易軌道検測装置を用いた静的軌道変位の測定の様子を示します．得られた静的軌道変位に対し，相互相関法を用いた位置合わせ³⁾を活用し，軌道検測車で得られる軌道変位から静的軌道変位を差し引く処理を行います．
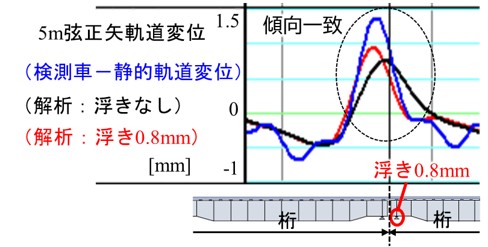
　図5に，実路線での軌道変位と解析結果の比較を示します．青色で示すのが軌道検測車で得られる軌道変位から静的軌道変位を差し引いて得られる実測データです．赤色で示す浮き0.8mmの数値解析結果は，青色の実測データと同様に支承あおり箇所で振幅が局所的に増大する傾向が得られており，数値解析の妥当性を確認できます．さらに，このような支承あおり箇所で振幅が増大する性質を利用することで，軌道変位の振幅が一定値以上となる場合に支承あおり有り，それ以下の場合には支承あおり無しとする簡易な支承あおり検知法を提案できます．

4．実路線での支承あおり検知結果

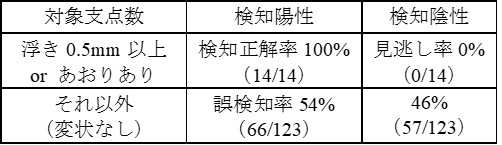
　提案する支承あおり検知法を実路線で検証しました．直結軌道の単純支持鋼橋が多数連続する実路線区間のうち，137箇所を支承あおり検知の対象としました．ここでは，鉄道事業者から提供された過去の目視点検のうち，浮き0.5mm以上の支承，または浮き量は不明であるもののあおりのみが確認されている支承を検知できるか検証します．
　表1に，実路線での支承あおり検知結果を示します．浮き0.5mm以上の支承またはあおりのみ確認されている支承の計14箇所はすべて検知陽性（支承あおり有りと判定）で，検知正解率は100%となりました．このことから，支承あおり箇所は見逃しなく検知可能であることが分かります．一方で，それ以外の変状が確認されていない箇所について，54%の箇所を誤検知しています．これは変状がない箇所も過剰に検出してしまう可能性もあり，精度向上に向けて現在検証を進めています．

5．おわりに

　本手法は，長大橋など鋼直結軌道を有する鋼橋が連続する区間に適用可能であり，目視検査が必要となる支承あおり箇所のスクリーニング・省力化にご活用いただけます．今後，鋼直結軌道に限らない在来線一般の橋りょう区間への適用範囲の拡大を検討します．

参考文献

1)国土交通省鉄道局監修，鉄道総合技術研究所編：鉄道構造物等維持管理標準・同解説（構造物編　鋼・合成構造物）－平成29 年付属資料改訂版－，丸善出版，2017．
2)服部他：数値解析による車上計測された軌道変位に橋りょう支承あおりが及ぼす影響評価，鉄道総研報告，Vol. 39，No.3，pp.31-38，2025．
3)田中他：相互相関法を応用した高頻度軌道検測データによる急進把握手法の開発，鉄道工学シンポジウム論文集，Vol. 21，pp. 1-8，2017.

執筆者：鉄道力学研究部　　　構造力学研究室　　　　　服部紘司
担当者：情報通信技術研究部　情報解析研究室　　　　　松岡弘大
　　　　構造物技術研究部　　コンクリート構造研究室　中田悠貴

都市部掘削工事における地盤改良体による盤ぶくれ対策工

1．はじめに

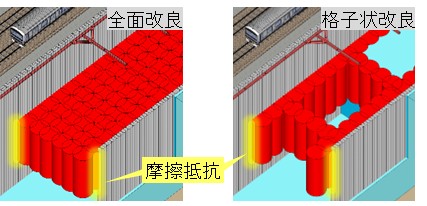
　鉄道地下トンネル建設時や鉄道近傍での掘削工事で用いられる掘削土留め工の設計では，盤ぶくれ等に対する掘削底盤の安定に対する検討が必要となります．盤ぶくれの検討を満足しない場合に実施される地盤改良は盤ぶくれ対策工のひとつであり，これには地盤改良体で止水壁や難透水層を造成する方法のほかに，掘削底面付近を改良して根入れ部における摩擦抵抗の向上を図る方法があります．このような場合，部分的に改良することで施工量を低減できる可能性が期待されます（図1）．本報では，模型実験と2次元FEM解析により，格子状に部分改良した掘削底盤の挙動を明らかするともに，得られた知見をもとにした格子状改良の設計手法を紹介いたします¹⁾．

2．揚圧力が作用する掘削底盤を模擬した模型実験

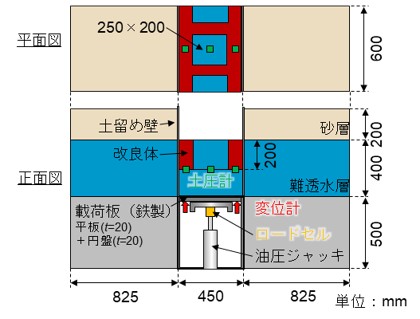
　十分に剛な載荷板を介して揚圧力を模擬した鉛直上向きの等分布荷重を漸増載荷することで，盤ぶくれを模擬した模型実験を実施しました．試験は無対策，全面改良，格子状改良の3ケースとし，模型実験の概要を図2に示します．格子状改良の改良率は65%としました．
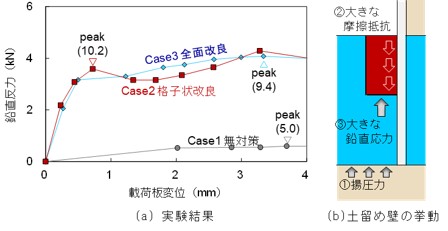
　各ケースの載荷で得られた載荷板変位と鉛直反力の関係を図3に示します．(a)図から，Case1の無対策と比べ，Case2の格子状改良では鉛直反力が大きく増加しており，Case3の全面改良と同程度となっていることがわかります．実験では難透水層および改良体の各位置での鉛直応力を測定しており，その値を分析するとCase2では改良体で大きな鉛直応力が発生していました．(b)図に示すように格子状改良における土留め壁模型との境界面において，全面改良と同様に摩擦抵抗が向上したものと考えられます．

3．FEM解析による掘削過程における格子状改良の効果の把握

　模型実験とは異なり，実際の掘削工事では難透水層上面で除荷が生じます．これに伴う格子状改良の効果を2次元土－水連成弾塑性FEM解析により把握しました．幅11mの領域を深度11mまで掘削する条件で，無対策，全面改良，格子状改良に加えて，格子状改良の非改良幅の掘削幅6mを加えた4ケースの解析を実施しました．
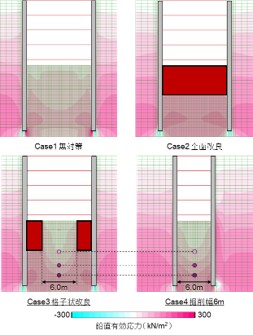
　最終掘削後十分時間が経過した時点における掘削底面の鉛直変位分布を図4に示します．無対策のCase 1と比較して全面改良のCase 2では掘削底面の鉛直変位が抑制されていますが，格子状改良のCase 3でも改良体位置では全面改良と同程度に掘削底面の変位が抑制されています．掘削幅6 mのCase 4の変位分布はCase 3の非改良部の変位分布と同様の傾向となることがわかりました．また，掘削底盤の鉛直有効応力分布を図5に示します．全面改良のCase 2では無対策のCase 1よりも改良体下面深度において大きな鉛直有効応力が残存しており，格子状改良のCase3でも改良体直下の鉛直有効応力は全面改良と同程度の値となり，掘削幅6 mのCase 4と深度方向の分布は同様の傾向となることがわかりました．以上の解析から，格子状改良でも改良体が盤ぶくれ対策効果を発揮すること，非改良部は同じ掘削幅の地盤の挙動と同等となることがいえます．

4．荷重つりあいによる格子状改良の試設計

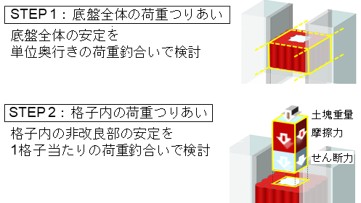
　模型実験および数値解析で得られた知見を踏まえ，従来の盤ぶくれに対する安定検討で用いられる荷重つりあいを指標とする格子状改良の盤ぶくれ検討手法を設定いたしました．その概要を図6に示します．本手順は，底盤全体，格子内の鉛直方向のつりあいをそれぞれ検討するとしました．STEP1では，底盤全体の荷重つりあいを単位奥行きで検討します．その際，改良体位置の摩擦抵抗は改良工法に応じた粘着力と安全率を用いて算出することとします．次にSTEP2では，格子内の非改良部の荷重つりあいを1格子あたりで検討します．その際，改良体と原地盤の境界における摩擦抵抗は原地盤の値を用いることとし，立坑等の閉じた領域の掘削では格子内の4面分の摩擦抵抗等を考慮することとしました．なお，本検討の適用条件としては，①掘削工事の規模が複線の鉄道の駅間トンネル程度であることと，掘削幅Bと改良厚Hの比率B/Hが2以下となることを目安としました．
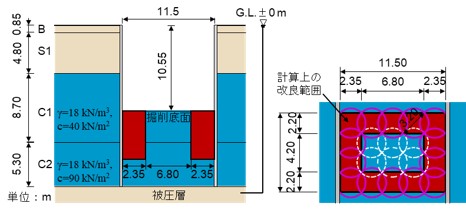
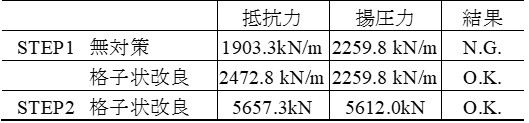
　図7に示す断面を例に，盤ぶくれの検討を行った結果を表1に示します．本検討では，改良率71%の格子状改良で盤ぶくれの検討を満足するという計算結果を得ることができました．

5．おわりに

　格子状の地盤改良が盤ぶくれ対策となり得ること，また設定した検討手法による設計が可能であることを確認いたしました．なお，格子状改良を考慮した盤ぶくれ対策の詳細な検討例は，「掘削土留め工の設計計算例」（鉄道技術推進センターHPで公開）に収録しています．併せてご参照ください．

参考文献

1)牛田ら：掘削工事における盤ぶくれ対策として格子状に地盤改良した掘削底盤の挙動，土木学会論文集，Vol.80，No.8，24-00067，2024.

執筆者：構造物技術研究部　基礎・土構造研究室　松丸貴樹
担当者：構造物技術研究部　基礎・土構造研究室　佐藤武斗，杉本英治
　　　　構造物技術研究部　トンネル研究室　牛田貴士

多変量解析を用いた線区の特性分析

1．はじめに

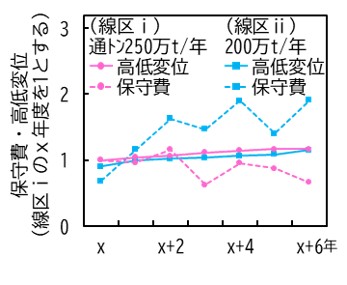
　少子高齢化と労働人口減少が進展する中，より効率的で効果的な軌道保守や設備投資が求められます．線区における保守費の投入効果の差を表す例として，図1に同じ線路等級の2線区の高低変位と保守費の推移を示します．保守費と高低変位は共に，線区ⅰの1年目を1とします．線区ⅰと線区ⅱの高低変位は同程度で推移していますが，保守費については，線区ⅰは一定または微減なのに対し，線区ⅱは徐々に増加しています．このように，同程度の軌道状態であっても，各線区における保守費の傾向は異なっていることから，軌道保守等の効率性向上には，各線区における特性を定量的に評価することが求められます．

2．主成分分析による線区特性の定量評価

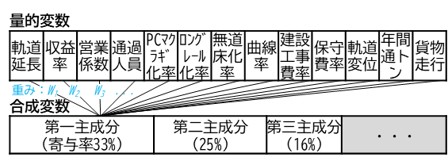
　主成分分析とは，多数の量的変数を合成してより少ない合成変数（主成分）に要約し，データが持つ情報をできる限り損なわずにデータ全体の特性を可視化する手法です．図2に，各線区において求めた13変数と，それら変数を合成した結果を示します．寄与率とは，主成分が持つ情報の大きさの比率です．図3に，寄与率の大きい第一主成分と第二主成分を構成する各変数の重みの分布を示します．第一主成分では収益や輸送量，軌道の強靭さに関する変数は正，営業係数や軌道変位に関する変数は負の相関関係にあることがわかります．これは，輸送量や収益等が大きいと営業係数や軌道変位は小さくなるという，線区の総合的な営業状態を表しています．第二主成分では，建設工事費を投入して軌道改良が進んでいる線区ほど，また曲線が少ないほど，軌道変位が小さくなるという関係を確認することができ，線区の総合的な軌道状態を表していると解釈することができます．
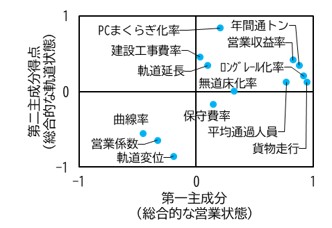
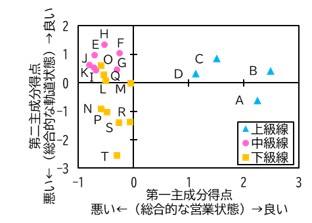
　図4に，A～Tの20線区の第一主成分と第二主成分に対する得点の分布を示します．この図より，各線区の位置づけを把握することができます．横軸は第一主成分，すなわち線区の総合的な営業状態を表す指標であることから，この図の右側に位置している線区ほど営業状態の良い線区であり，一方，左側に行くほど収入が低く営業状態が悪い線区であると評価することができます．また，縦軸の第二主成分は線区の総合的な軌道状態を表す指標であることから，上にいくほど軌道改良が進んでいて軌道変位が小さくなるということができます．図4の右の方に営業状態の良い上級線，下の方に軌道状態の悪い下級線が多く分布していることからも，本分析により線区の特性を表すことができていると考えられます．例えば下級線の線区Oについては，営業状態は良くないものの軌道状態の良い線区です．例えば軌道保守費などの限られたリソースを，営業状態を考慮して配分しなければならない場合，線区Oのように図の左上（第2象限）に含まれる線区は軌道保守量を削減するなどの方針や施策を検討することが可能です．

3．クラスタ分析による線路等級の検討

　クラスタ分析とは，各データが持つ情報に基づいていくつかのグループであるクラスタに分類する手法です．クラスタ分析には，階層クラスタ分析と非階層クラスタ分析の2種類があります．ここでは，最も近いデータ同士を順番にグループ化していき，徐々にクラスタの数を少なくしていく手法である階層クラスタ分析を採用しました．
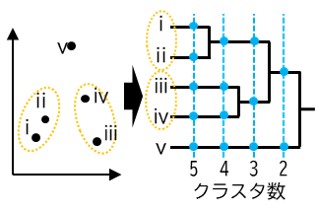
　図5に，点ⅰ～ⅴを階層クラスタ分析手法によりグループ化する場合のイメージ図を示します．これより，位置が近いものから順に結合，つまりグループ化されていく様子がわかります．例えばクラスタ数を3とする場合は，図中の点線で囲ったように，ⅰとⅱ，ⅲとⅳ，ⅴ単体の3つのグループに分類することができます．このクラスタを線路等級と読み替えることで，クラスタ分析により線路等級を検討することが可能です．
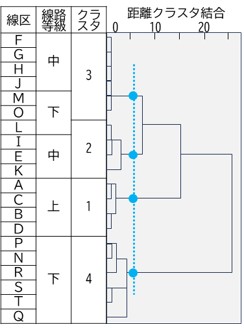
　図6に，上・中・下級線からなるA～Tの20線区に対して階層クラスタ分析を行い，線区がグループ化されていく結果を示します．ここでは，4つの変数（営業係数，保守費，軌道変位，貨物走行）を用いて，20線区を4つのクラスタに分類する例を示しています．クラスタの番号は，上級線区ほど小さく，下級線区ほど大きくなるように設定しました．上級線はすべてクラスタ1に分類されましたが，中級線はクラスタ2または3に分類されました．両者を比較すると，クラスタ2に分類された中級線に比べ，クラスタ3に分類された中級線は保守費が少なく，また高低変位も大きい線区でした．また，下級線については，クラスタ4に分類された線区がほとんどでしたが，一部の線区は，クラスタ2または3に分類されました．例えば，保守に関するリソースを削減しなければならない場合は，上位のクラスタに分類された中級線や下級線を対象として検討することが考えられます．一方，サービスレベル向上を検討する場合においては，例えばクラスタ2に分類された下級線の線区Lは，ニーズに応じて速度向上や軌道構造強化などの施策により，上級線や中級線相当として扱うことなども考えられます．

4．おわりに

　主成分分析とクラスタ分析を用いて，様々な実態を踏まえて線区の特性を定量的に評価する手法を開発しました．これにより，投資できるリソースを各線区や区間に適正に配分する際などにおいて，より効率的な施策の検討を行うことが可能となります．

参考文献

1)松本他：多変量解析手法を用いた線区特性の評価手法の開発，新線路，79巻，5号，pp.25-27，2025

執筆者・担当者：軌道技術研究部　軌道管理研究室　松本麻美

発行者：後藤　恵一　【(公財) 鉄道総合技術研究所　施設研究ニュース編集委員会　委員長】
編集者：藤川　理沙子　【(公財) 鉄道総合技術研究所　軌道技術研究部　軌道・路盤】