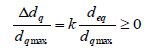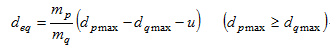施設研究ニュース
2018年7月号
細粒土混入バラストの造粒化による軌道補修工法の開発
1.はじめに
鉄道のバラスト軌道は,列車の繰返し載荷およびタイタンパを用いたつき固め補修により,道床の細粒化に伴い道床内部の細粒分含有率が高くなります.そのような状態になると,つき固め補修を行っても沈下が生じやすく,補修頻度が増大します.
そのため,細粒分含有率が高いバラスト道床に対して,道床更換を行うことが補修頻度低減の基本的な対策となりますが,道床更換はコストが高いため,軌道の維持管理コストを低減するためには,補修効果が持続する沈下抑制対策工が求められています.
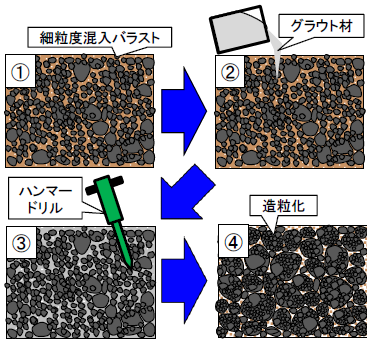
そこで,細粒土混入バラストに対してグラウト材を充填させ,固化した後に破砕させることで細粒土を造粒化させる工法(以下,造粒化工法)を開発しました(図1,図2).本研究では,実物大模型を用いた繰返し載荷試験により造粒化工法の補修効果を確認し,営業線での試験施工により補修効果を検証しましたので紹介します.
2.造粒化工法の概要
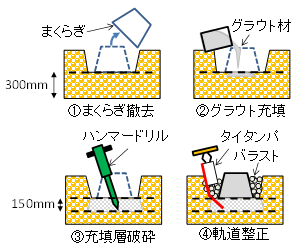
造粒化工法はセメント系のグラウト材を細粒土混入バラストに浸透させ,硬化した後にハンマードリルで破砕して細粒土を造粒化させる補修方法です.グラウト材は、細粒土混入率の高い既設のバラスト道床に対して,浸透性を確保できる超微粒子セメントミルクを用いました.造粒化工法の施工手順を図3に示します.
①施工区間のまくらぎを一旦撤去する.
②まくらぎ下面のバラスト表面に,超微粒子セメントミルクを自然流下で充填する.
③1時間の養生後に,ハンマードリルを用いてグラウト充填層を0.1m程度の粒径となるように破砕する.
④まくらぎを元の位置に戻して軌道復旧し,タイタンパによるつき固め補修により軌道整正する.
3.造粒化工法の実物大模型試験
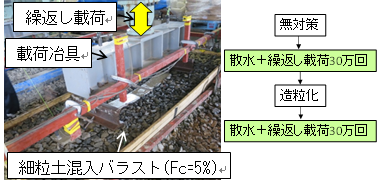
造粒化工法の補修効果を確認するため,実物大模型を用いた繰返し載荷試験を実施しました.実物大模型試験の載荷状況と試験手順を図4に示します.道床は細粒分含有率Fc=5%の細粒土混入バラストとしました.載荷条件は最小荷重5kNおよび最大荷重85kN(荷重振幅80kN)で,載荷周波数5Hzの正弦波としました.施工手順は,タイタンパによる通常のつき固め補修(無対策)後に散水,繰返し載荷30万回を実施しました.その後,造粒化工法を施工した後,さらに散水し,繰返し載荷30万回(計60万回)を行いました.繰返し載荷前に散水したのは,降雨による影響を考慮するためであり,3.1m×1.0mの範囲に93ℓの水を撒きました.
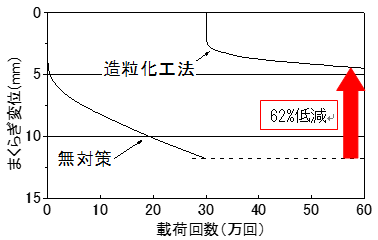
まくらぎ変位と載荷回数の関係を図5に示します.繰返し載荷30万回後のまくらぎ変位は,無対策の場合11.8mm,造粒化工法を施工することで4.5mmとなり,無対策と比べて造粒化後は62%低減しました.
4.営業線での現地試験施工
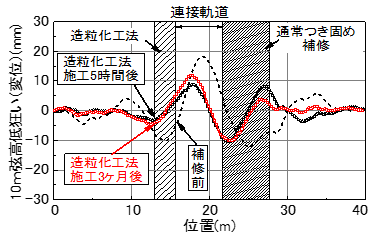
造粒化工法の補修効果を実軌道で検証するため,営業線での現地試験施工を行いました.試験施工箇所の状況を図6に示します.当該箇所は,噴泥までは至っていないがバラストの細粒土混入率が比較的高い(細粒分含有率Fc=8.5%)箇所でした.本工法施工に先立ち,事前にグラウト材がバラストに充填されることを確認しました.造粒化工法施工前後の10m弦高低狂い(変位)を図7に示します.本工法の比較対象として,本工法施工時にタイタンパによる通常のつき固め補修を踏切の反対側にて実施しました.補修前の高低狂い(変位)は最大10mm程度でしたが,造粒化工法施工5時間後(列車20本程度通過),造粒化工法箇所は最大4mm,通常つき固め箇所は最大10mmでした.また,造粒化工法施工3ヶ月後は,施工5時間後と概ね同等の高低狂い(変位)であり,造粒化工法は通常つき固め補修と比べて軌道補修効果が高いことを確認しました.
5.おわりに
細粒土混入バラストの軌道補修工法として造粒化工法を開発し,本工法が十分な軌道補修効果を有していることを確認しました.今後は,現地試験施工後の軌道検測データから補修効果の持続性を確認します.また,さらに試験施工実績を重ねて本工法の実用化を目指していく予定です.
執筆者:軌道技術研究部 軌道・路盤研究室 伊地知卓也
担当者:軌道技術研究部 軌道・路盤研究室 桃谷尚嗣,中村貴久,木次谷一平
津波に対する桁流失防止工法
1.はじめに
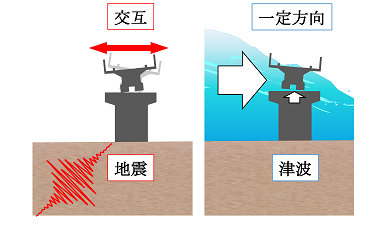
多くの鉄道RC構造物には耐震補強が施されていますが,津波は地震と異なる特徴があるため,津波等による桁流失被害が報告されています.例えば,図1のように桁は,地震では正負交互に揺れますが,津波では一定時間一方向押され,浮力により浮上ることもあります.また,津波の水平力は地震よりも大きい場合があります.加えて,津波は地震後に生じることが多く,地震の後に津波に抵抗することが期待されます.
本稿では,新設よりも施工上の制約が多い,既設鉄道コンクリート橋りょうを対象とした流失防止工法を開発したので紹介します.
2.桁流失防止工法の概要
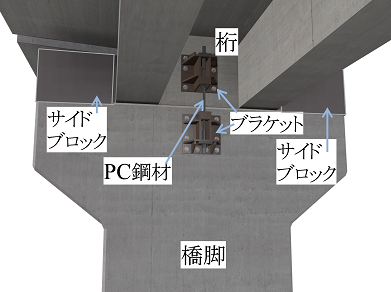
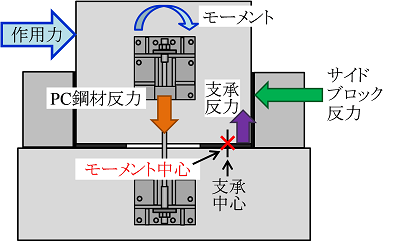
図2は,本工法で補強した橋りょうのイメージです.本工法では,地震の揺れに対する落橋防止装置として設置が進められているサイドブロックに加えて,桁と橋脚を連結するPC鋼材を次の手順で施工します.まず,アンカーを用いて上部鋼製ブラケットを横桁,下部鋼製ブラケットを橋脚に取付けます.続いて,上部・下部鋼製ブラケットに,PC鋼材を設置します.その後,桁横に緩衝ゴムを設置し,それを型枠の一部として桁横にサイドブロックを打設します.
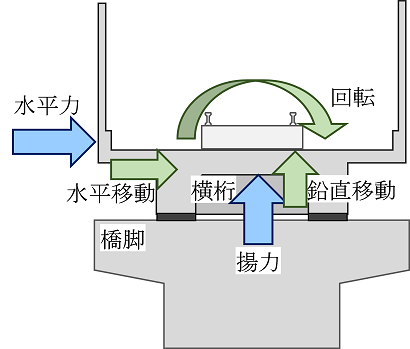
桁流失被害は,図3のように津波により桁に生じた水平力および揚力が,桁を水平移動,鉛直移動,回転させることで生じると指摘されています.本工法では,津波による水平移動に対してはサイドブロックで,鉛直移動と回転に対してはPC鋼材で抵抗します.また,大きな衝撃力に対しては,サイドブロックと桁の遊間に設置した緩衝ゴムで力を分散します.このように,移動や回転を生じさせる各々の力に対して,抵抗する部材を分離・独立して考えることで,設計の単純化と橋りょうに到達する津波の規模や特性に応じた最適な断面の設定ができます.
本工法は,地震の揺れに対しては,橋軸直角方向はサイドブロックで,橋軸方向は橋脚に取り付けたブラケットで落橋を防止します.常時の桁の収縮や温度伸縮に対しては,PC鋼材とブラケットの接続部を拘束せず,橋軸方向に動ける仕様とすることで対応します.
3.提案工法の耐荷機構の確認
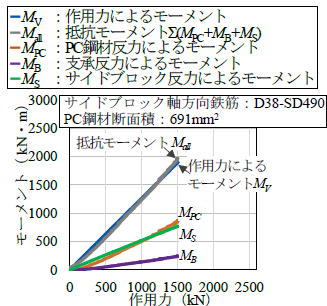
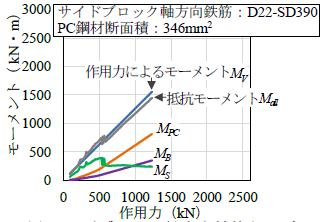
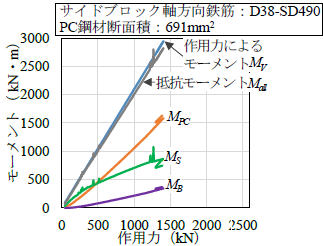
図4のように橋軸直角方向の桁座寸法が十分に確保された長さ30m,高さ1.8m,幅5.7mの鉄道コンクリート橋りょうを想定した実物大の載荷試験を行いました1).この結果,本工法により補強された橋りょうは,東日本大震災クラスの津波(波高20m,流速6m/秒)に相当する力(約1100kN)を上回る1500kN以上の水平力に対して桁の流失を防止できることがわかりました.また,1500kN作用時にも鉄筋の降伏やコンクリートの圧縮破壊がみられないこと等から,コンクリートの弾性挙動と桁の剛体回転を仮定することで,本工法で補強した橋りょうは作用力に対して主に図5に示す反力で抵抗すると推定しました.図6(a)は図5に基づき下流側ゴム支承中心まわりのモーメントを算出したものです.図6(a)から,津波により補強された橋りょうに生じるモーメントと,PC鋼材やサイドブロック等の反力によるモーメントの総和が等しいことを確認しました.
また,有限要素法解析により,耐力について,PC鋼材の直径を小さくした場合とサイドブロックの軸方向鉄筋の降伏強度を低下させた場合の耐荷機構を検討しました.さらに,作用力について,実験の想定と規模の異なる津波として,作用力の方向が異なる場合の耐荷機構も検討しました.その結果,図6のように,想定した耐力と作用の範囲では,実験と同様に,津波により補強された橋りょうに生じるモーメントと,PC鋼材やサイドブロック等の反力によるモーメントの総和が等しいことを確認しました.したがって,作用する波の特性に応じた桁の流失対策が可能であると考えられます.
図6 下流側ゴム支承中心まわりのモーメント-作用力関係
4. おわりに
本稿では,今後の発生が危惧される巨大津波による被害低減法として,既設鉄道コンクリート橋りょうを対象とした流失防止工法を紹介し,その耐荷機構を示しました.本工法は,近年も被害報告がある河川増水による桁流失対策や道路橋への適用も可能であり,今後,鉄道事業者だけでなく,道路の管理者へも本工法の紹介および普及をすすめる所存です.なお,本研究の一部は,国土交通省の鉄道技術開発費補助金を受けて実施しました.
参考文献
1) 佐藤祐子・渡辺健・轟俊太朗・大野又稔:津波作用抵抗機構を考慮した桁流失防止工法の開発,総研報告,Vol.32,Vol.7,p.41-46,2018
執筆者:構造物技術研究部 コンクリート構造研究室 佐藤祐子
担当者:構造物技術研究部 コンクリート構造研究室 渡辺健,轟俊太朗
鉄道RC高架橋相互の地震時繰り返し衝突を考慮した耐震設計法
1.はじめに
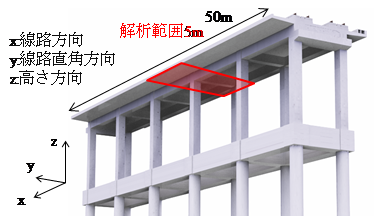
鉄道分野では,複数路線を有する駅部において,駅部ホームや前後の高架橋が橋軸直角方向に近接して配置される場合があります.このような近接した高架橋間の遊間は一般的に10~300mm程度であることから,線路直角方向の地震時挙動を考えた場合,L1地震時でも高架橋応答の位相差によっては,高架橋の張出スラブが相互に衝突により,上部工の損傷や構造物全体系の応答増幅が発生する可能性があります.本稿では,鉄道RC高架橋相互の地震時繰り返し衝突を考慮した耐震設計法を提案しました1).
2.張出スラブの地震時衝突時の接触現象の解明
(1) 詳細モデルによる衝突解析
鉄道高架橋の線路直角方向の衝突を考えた場合,張出スラブが相互に衝突すると想定されることから,赤枠に示す上部工範囲をモデル化し,二つのモデルを隣接させて衝突解析を行いました(図1).
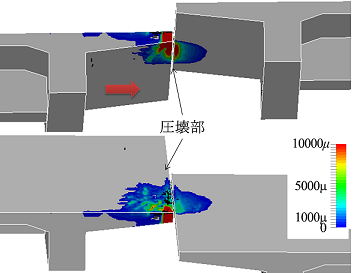
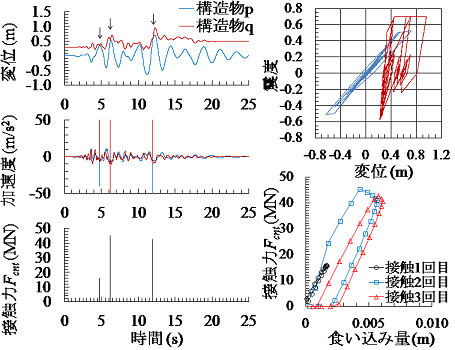
図2は,衝突解析で得られた衝突後のひび割れ分布図および圧壊部を示しています.衝突速度や衝突角度により程度は異なりますが,張出スラブが鉛直上方向にたわむことにより付け根部にひび割れが発生すること,加えて線路方向に5mの領域に亘って接触部近傍で圧壊を起こすことが明らかとなりました.
(2) 簡易接触モデルの提案
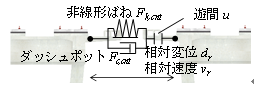
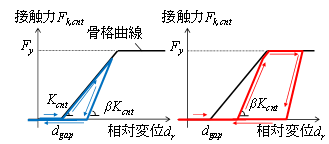
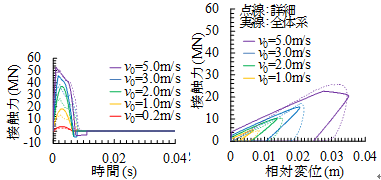
詳細な衝突解析は計算コストが高く一般的な耐震設計で用いることは難しいことから,上部工相互の衝突によるエネルギー損失を簡易に考慮できる接触モデルを構築しました(図3).簡易モデルでは,材料の非線形化により損失される履歴エネルギーを非線形ばねにより,振動エネルギーに変換されるエネルギーをダッシュポットにより表現します.本モデルにより,接触速度5m/s2まで,接触角度10mradまでの範囲で,接触力や食い込み量等の非線形特性を再現できることを示しました(図4).
図3 簡易接触モデル
3.高架橋の繰り返し衝突を考慮した地震時応答評価
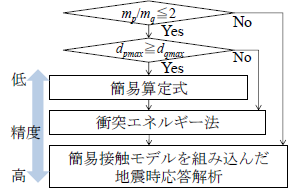
ここでは、設計者がニーズに合せて使い分けられるよう,応答予測精度に応じて,上記した簡易接触モデルによる応答解析,衝突エネルギー法,簡易算定式の3つの方法を提案しました.
(1) 簡易接触モデルを用いた地震応答解析
簡易接触モデルは,2構造物の接触を直接考慮しながら非線形時刻歴応答解析を実施する最も適用範囲の広い手法です(図6).
(2) 衝突エネルギー法
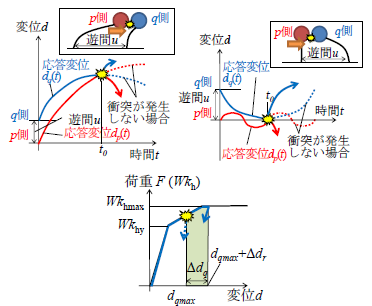
衝突エネルギー法は,代表的なシナリオを仮定して,個々の最大応答変位等のパラメータに基づき,運動エネルギーと復元力による履歴エネルギーの釣り合いを考慮して,2構造物の接触による応答増幅Δdqを算出する手法です(図7).
(3) 簡易算定式
簡易算定式は,2構造物の衝突を考慮しない場合の最大応答変位dpmax,dqmaxおよび遊間uに基づき,応答増幅Δdqを算定するものです.
ここで,kは地震動の規模に依存する係数でL1地震時には1,L2地震時には2とします.また,deqは、2構造物の質量mp,mqの関数である次式により算出されます.
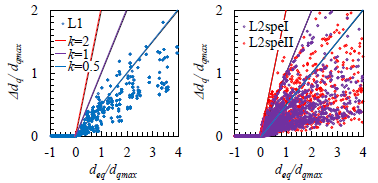
簡易算定式は,衝突エネルギー法と比較して応答を安全側に評価しますが,最も簡単な手法です(図8).2構造物の質量比が大きく異なる場合は,簡易算定式,衝突エネルギー法の推定精度が著しく低下することから,簡易接触モデルによる衝突解析を行う必要があります.
4.おわりに
本研究では,高架橋の張出スラブの地震時衝突時の接触現象の解明や実用的な設計法の整備を行いました.本研究の成果が一助となれば幸いです.
参考文献
1)徳永 宗正, 曽我部 正道, 鉄道RC高架橋相互の地震時繰り返し衝突を考慮した耐震設計法, 土木学会論文集A1(構造・地震工学),Vol.74,No.1,pp.173-185,2018.
執筆、担当者:鉄道力学研究部 構造力学研究室 徳永宗正