機械学習を用いた列車混雑予測手法
1.概要
ダイヤ乱れ時に混雑予測情報を旅客に提供できれば、旅客の快適性低下の防止に繋げることができると考えられます。そこで、大都市通勤路線において、1時間程度の運転見合わせが発生し、そこから運転を再開した後、遅延が収束するまでを対象に、5つの予測手法を用いて列車混雑予測モデルを構築しました。実際のダイヤ乱れ事象を対象に、その予測精度を2つの評価指標(再現率・適合率)を用いて比較し、各手法が得意・不得意とする予測時間帯や予測対象駅などの条件や、予測結果の精度特性を明らかにすることを試みました。
なお、本成果に関する発表により、2024年度に情報処理学会ITS研究会より優秀発表賞を受賞しました。
2.列車混雑を予測するまでの流れ
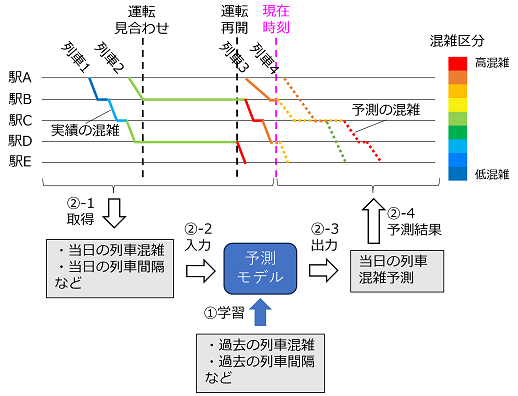
列車混雑の予測は、①過去のデータを用いた予測モデルの学習と、②ダイヤ乱れ当日の現在時刻までの実績データから現在時刻以降の列車混雑を予測する2つの処理を行います(図 1)。予測モデルの学習では、過去の列車混雑や列車間隔から、データ間の関係性や法則性を学習し、予測モデルを構築します。そして、ダイヤ乱れ当日に、現在時刻までの実績の列車混雑や列車間隔を学習済みの予測モデルに入力し、現在時刻以降の予測混雑が出力されます。この処理を、各列車が各駅を発車する度に行うことで、直近の実績データを反映した混雑予測結果を常に保持するようにします。
3.5つの予測手法を用いた列車混雑予測モデルと入出力データ
列車混雑予測モデル構築にあたり、以下の3種類の機械学習手法と、機械学習以外の2種類の手法を選定し、各手法を用いたモデルの入出力データを選定しました。
ニューラルネットワーク(NN)
NNは、人間の脳の神経細胞網の働きを計算機上で疑似的に扱えるようにモデル化したものです。一つ一つの神経細胞をパーセプトロンと呼ばれる計算モデルで表し、NNはパーセプトロンが複雑に結合したネットワークになります。本研究では、3層構造のフィードフォワード型ニューラルネットワークを用います。
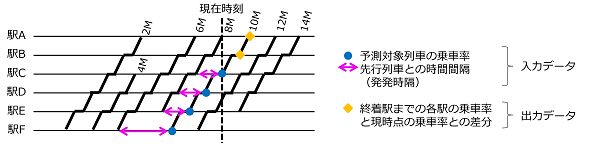
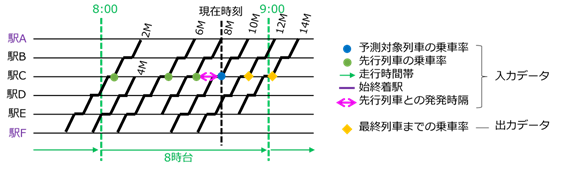
予測モデルは、駅・方面・時間帯毎に別々のモデルを用意して学習し、当日に対応する予測モデルで予測することで、平常時と列車運行時刻が大幅に異なるダイヤ乱れ時の予測精度を向上させています。NNの入出力データは、混雑に影響すると考えられる複数の入力データから、最も高精度に予測できる入出力データの組み合わせを選定しました(図 2)。特に、出力データを予測対象列車の終着駅までの乗車率と現在時刻時点の乗車率との差分値とすることで、平常時と乗車率の値が大幅に異なるダイヤ乱れ時の予測精度を向上させています。
LightGBM
LightGBMは、決定木ベースの教師あり学習手法です。アンサンブル学習の一種である勾配ブースティング手法を用いることにより、従来の決定木を用いた手法よりも高精度に予測できます。
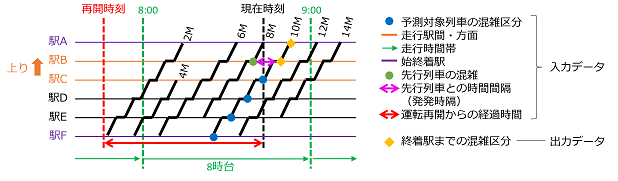
予測モデルは、全列車の全駅発時点で共通のモデルを使います。入出力データは、NNなどの他の予測手法よりも多重共線性の影響が比較的少ない決定木ベースの手法の特徴を活かし、決定木ベースの「運転再開からの経過時間」のようなダイヤ乱れ時特有の、混雑に影響すると考えられる特徴量を入力データとし、学習・予測を行います。出力データは、乗車率0%~250%を25%区切りで9つに分割した混雑区分(図 3)です。図 4に入出力データを示します。
サポートベクターマシン(SVM)
異なるクラスに属するデータ間に境界線を設定し、データがどのクラスに属するかを予測する手法です。予測モデルは、LightGBMと同様に全列車の全駅発時点で共通のモデルを使い、入出力データもLightGBMと同じ、図 4に示したデータを用います。
ARIMAX
自己回帰モデルと移動平均モデルを組み合わせた時系列データ予測手法であるARIMAのモデルに、外部要因の影響を外生変数として組み込んだモデルです。
ARIMAXは、まず、各駅において同じ方面に発車する各列車の乗車率を時系列データとみなし、予測モデルを構築します。つまり、駅・方面毎にモデルを用意します。図 5では、先行列車を含む自列車10Mまでの駅C発車時の乗車率を入力データとし、後続列車12M以降の駅C発車時の乗車率を予測、出力します。さらに、列車の混雑に影響を与える、先行列車との時間間隔や走行時間帯といった要素を外生変数としてモデルの入力データに含めます。
重回帰分析
複数の説明変数から目的変数を予測するモデルです。重回帰分析は、多重共線性の影響が大きいと考えられることから、少ないデータ種類数で高精度に予測できる入出力データが望ましいと考え、NNと同じ入出力データを用います。
4.5つの予測手法を用いたモデルの精度特性の分析
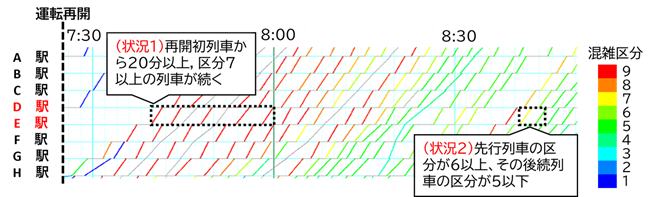
ある大都市通勤路線を対象に、ダイヤ乱れ時に実際に発生している2つの混雑状況(図 6)に着目し、これらの状況をどれほど予測できているかを再現率と適合率の2つの評価指標を用いて検証しました。なお、再現率は、検出漏れがどれほど少なかったかを表す指標であり、適合率は、誤検出がどれほど少なかったかを表す指標です。
(状況1)ある列車・駅発時点において、当該駅で20分後までに発車する全列車の混雑区分が7以上。
(状況2)ある列車・駅発時点において、当該駅の後続列車の混雑区分が6以上、さらに次の後続列車が5以下。
学習・予測データには、ある事象により運転を見合わせた、平日30日分のデータを用いました。本検証では、学習データと予測データの日付の前後に関係なく、29日分を用いてモデルを学習させ、残りの1日分に対して予測精度を検証しました。30日分のデータの中で、状況1は288件、状況2は933件存在し、本検証ではこれらを、①走行時間帯、②予測対象駅、③運転再開からの経過時間、④運転見合わせ時間、⑤事象発生区間毎に、再現率と適合率を算出しました。
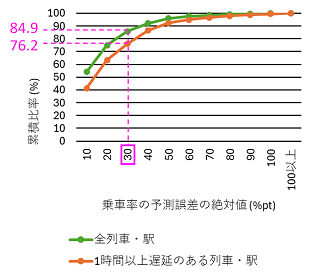
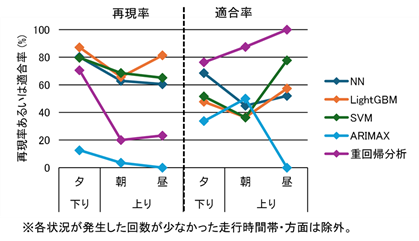
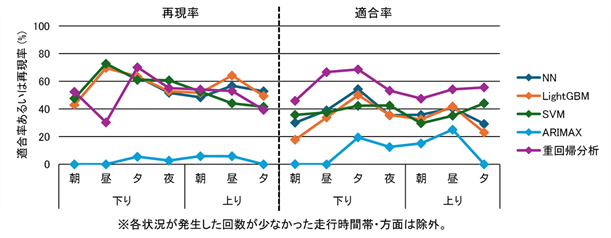
①~⑤のうち、①の結果について、状況1を図 7、状況2を図 8に示します。ARIMAXは、状況1、2とも精度が低く、モデル自体のさらなる精査が必要であることが分かりました。ARIMAXを除く4手法で比較すると、図 7から、状況1では、再現率は機械学習手法の方が重回帰分析よりも高精度で、適合率は逆に重回帰分析の方が高精度な傾向が見られました。また、図 8から、状況2では、再現率は手法間でほぼ差が見られないものの、適合率は方面・時間帯に関係なく、重回帰分析の方が機械学習手法よりも高い傾向が見られました。②~⑤に関しても、ほぼ同じ傾向が見られたことから、列車混雑予測において再現率を重視する場合は機械学習手法、適合率を重視する場合は重回帰分析のように、重視したい指標に応じて、適用する手法を使い分けることが有用であることが示唆されました。
今後は、得られた精度特性を踏まえ、用途に応じた適用手法の有用な使い分け方法を検討するなど、実用性のある列車混雑予測を検討していく予定です。
参考文献
- 上田寛人,中挾晃介,國松武俊:LightGBMを用いたダイヤ乱れ時の列車混雑区分予測モデルの検討,情報処理学会第97回ITS研究発表会,[MBL/ITS]機械学習(3),2024
- 中挾晃介,上田寛人,國松武俊,武内陽子,辰井大祐:ダイヤ乱れ時の列車運行時刻の変化に対応したニューラルネットワークによる列車混雑予測手法,情報処理学会第98回ITS研究発表会,[一般講演セッション1](4),2024
- 中挾晃介,上田寛人,國松武俊,武内陽子,辰井大祐:機械学習を用いたダイヤ乱れ時の列車混雑予測手法の精度特性の分析,情報処理学会第87回全国大会,ネットワーク(交通システムとドライバー)5D-03,2025